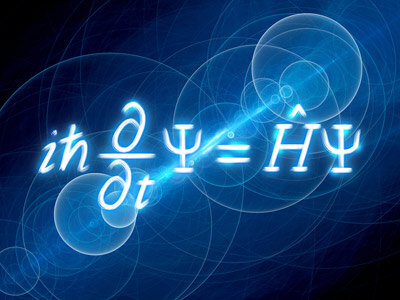The number of measurements needed to characterize a system of quantum particles is far fewer than previously thought, a RIKEN physicist and three collaborators have shown. As well as cutting the workload of experimentalists, this finding has important repercussions for verifying emerging quantum technologies such as quantum computing.
All the objects surrounding us are collections of quantum particles held together by electromagnetic forces. These forces can be expressed by remarkably simple equations. Complexity arises because interactions among particles yield non-trivial quantum phenomena that cannot be expressed in terms of one-particle behavior.
“The world we live in is governed by the Schrodinger equation,” explains Tomotaka Kuwahara of the RIKEN Center for Advanced Intelligence Project. “In principle, we can clarify all phenomena in nature by solving this equation. But to obtain the Schrodinger equation, you need to know the Hamiltonian (that is, the energy matrix), which depends on the details of the system.”
The Hamiltonian can be determined by performing repeated measurements on a quantum system. But, with existing algorithms, the number of measurements increases exponentially with the number of particles making up the system, which makes for a prohibitively high number of experiments.
Now, Kuwahara and three collaborators at IBM, UC Berkley and MIT in the United States have developed a machine-learning algorithm for which the number of required measurements increases as the cube of the number of particles. Their setup considers the experimentally relevant situation of how many copies of the Gibbs state of a target Hamiltonian are needed to determine the Hamiltonian. For a system of 15 particles, that’s roughly 3,000 measurements instead of about 30,000, while for a 100-particle system, it’s 1,000,000 measurements instead of a whopping 1029.
Surprisingly, the result applies even to low-temperature systems, whose thermal equilibrium states usually have highly complicated structures.
This advance has important ramifications for quantum computers. “In quantum computing, we often need to identify the system Hamiltonian for verification; such verification is a critical problem for the reliable implementation of quantum algorithms,” says Kuwahara. “Our result can be used to verify some important quantum algorithms.”
The researchers also anticipate that their algorithm could be used to investigate the properties of quantum materials by performing quantum measurements. “One application of our method is to use it to elucidate the properties of exotic quantum systems that are realized in complex setups such as ultracold-atom or trapped-ion experiments,” says Kuwahara.
The team now intends to extend their work in two directions. “Using our current techniques, we may be able to clarify the sample complexity of other learning problems,” says Kuwahara. “We also want to improve our algorithm so that it’s not only sample efficient but also time efficient.”
More information:
Anurag Anshu et al, Sample-efficient learning of interacting quantum systems, Nature Physics (2021). DOI: 10.1038/s41567-021-01232-0
Citation:
Determining the Hamiltonian of quantum systems with far fewer measurements (2022, January 13)