Topological ideas have recently taken the center stage of modern electromagnetics. Typical topological photonic systems are based on nonreciprocal materials, a class of materials that enables asymmetric light–matter interactions. In particular, nonreciprocal platforms may support unidirectional channels that allow propagation in a given direction of space—let’s say from left to right, but not the other way around. Such unidirectional guides are of key importance in optical systems because their modular designs involve one-way interactions that require the optical isolation of the different modules.
Even though the topological properties of a material are rooted in abstract mathematical concepts, they can be distilled in a simple physical way. Consider the problem of interfacing a number of different nonreciprocal materials—let’s say five, for example, at some junction point, like slices of a pie. All the materials operate in a frequency band gap where they do not support propagation in their bulk regions. However, each of the interfaces may support a certain number of unidirectional edge states, which can propagate either towards the junction point or away from it.
Stating that a system is topological is a sophisticated way of saying that, in the described situation of the pie-like interfaced materials, it is impossible to devise a construction where the number of incoming radiation channels differs from the number of outgoing channels. In other words, in topological systems there is forcibly a balance between the number of incoming channels and the number of outgoing channels, analogous to the conservation of current in Kirchhoff’s circuit laws. In fact, if the number of incoming and outgoing channels could be different, then it would be possible to devise an excitation which would continuously transfer energy from a source to the junction point. In such a situation, a thermodynamic equilibrium can be reached only if the energy arriving at the junction is dissipated as heat.
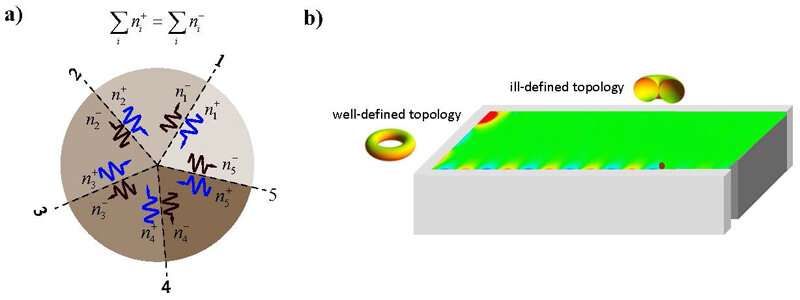
a) Junction between different bulk materials that share a common band-gap. In a topological system, the number of incoming edge channels and the number of outgoing edge channels is exactly the same. b) A system with an ill-defined topology is not bound by that constraint. The ill-defined topology can be used to abruptly halt wave propagation at a topological singularity. © D. Fernandes and M. Silveirinha, Tecnico Lisboa.
Now, as reported in Advanced Photonics, researchers have shown that such a contrived scenario can indeed be observed in realistic physical systems. They explore the fact that nonreciprocal systems with a continuous translation symmetry have an ill-defined topology. They demonstrate that, contrary to common belief, a junction of nonreciprocal materials is not necessarily bound by any balancing constraint on the number of in/out channels.
The team experimentally verified that, by pairing two waveguides, one with an ill-defined topology, and another with a well-defined topology, it is possible to bring an edge mode to an immediate halt at the junction between the waveguides, creating a topological singularity. The wave is stopped in its tracks at the singularity, which can be pictured as an energy sink where all the incoming energy is concentrated and eventually dissipated at a single point in space. These exciting developments suggest a new way to achieve topological singularities that feature extreme wave phenomena. This may be useful for energy harvesting and to enhance nonlinear effects.
More information:
David E. Fernandes et al, Experimental verification of ill-defined topologies and energy sinks in electromagnetic continua, Advanced Photonics (2022). DOI: 10.1117/1.AP.4.3.035003
Citation:
Halting a wave in its tracks (2022, May 23)