Sometimes, the most complex problems can be solved with the simplest approaches. Such was the case for researchers at UC Santa Barbara as they tried to resolve a longstanding issue of fluid friction—the resistance between an object moving through fluid, or conversely, a stationary object with fluid flowing around or through it. It’s also known as drag.
“We had built a theory, but it was a very messy problem,” said mechanical engineering professor Paolo Luzzatto-Fegiz. Their problem dealt in particular with superhydrophobic surfaces (SHS), which are seen as a potential solution to the problem of drag, a phenomenon that reduces the efficiency of things traveling through water, like cargo ships, and increases the energy expenditure to pump liquids through pipes.
Their calculations for an effective SHS encompassed 10 complex parameters, but as it turns out, the ability to predict if an SHS will perform as intended boils down to just one. Their research is published in the Proceedings of the National Academy of Sciences.
Getting into the groove
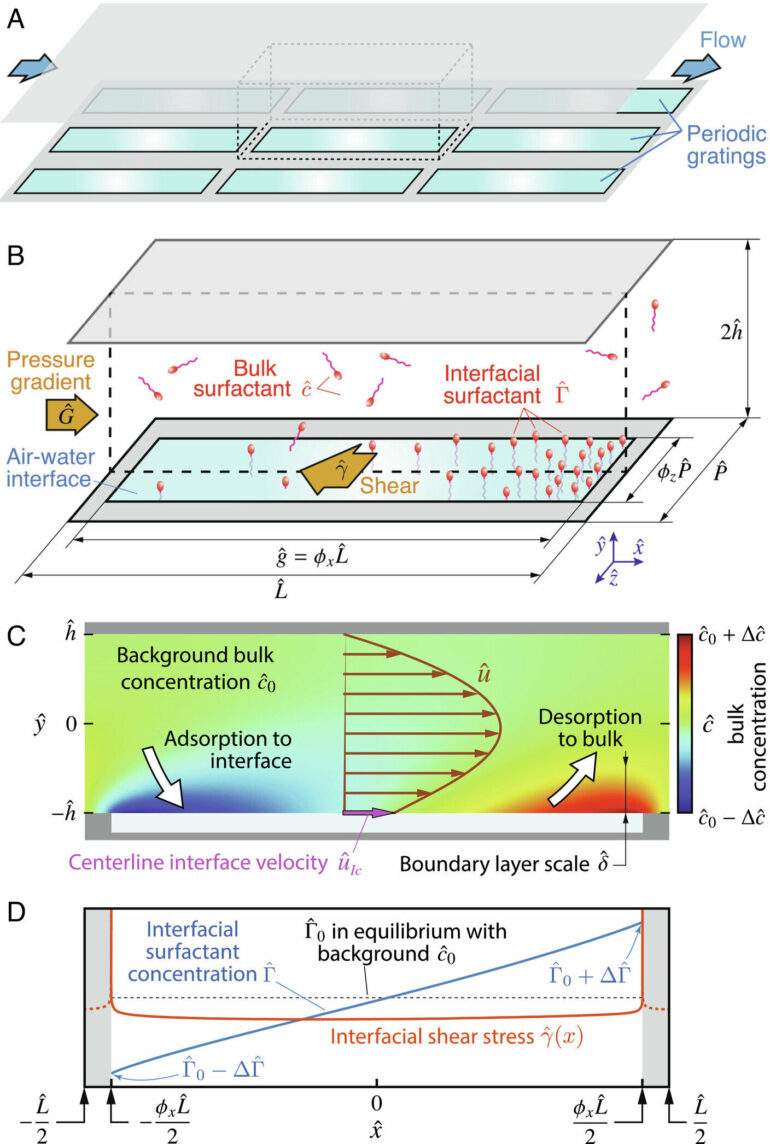
A superhydrophobic surface, Luzzatto-Fegiz explained, is designed to minimize contact between the surface and the fluid by creating tiny pockets of air. A good example of this would be fresh kale, when dunked in water. Thanks to microscopic surface structures, the leaves would be covered in a silvery sheen—a network of bubbles that prevents water from touching the leaf’s surface, also known as the lotus effect.
For plants, superhydrophobicity results in a self-cleaning effect, and helps prevent waterborne conditions such as fungal infections. For inanimate surfaces, the same property reduces drag. But while the concept is sound, in practice, surface patterning did not have the desired effect due to surfactants, compounds that reduce the tension between the water and the air in the bubbles. In real-world situations, Luzzatto-Fegiz said, surfactants are unavoidable, and even a trace amount can be enough to negate the performance of an SHS.
In their effort to design a surface that overcomes the effect of surfactants, the researchers had to contend with complex calculations involving not just fluid mechanics (already complicated), but also the physics of the surfactant molecules.
“We needed models for how these things moved inside the water, how they hop from inside the water to the interface, how they’re transported,” he said. But over the course of their experiments, modeling and computation, one parameter emerged that seemed to override all the others: the length of the air bubbles.
“When we looked at the math, we decided to restrict ourselves to things that could plausibly happen,” Luzzatto-Fegiz said. “A lot of the parameters couldn’t change that much in reality.” With this constraint, they realized that several factors could cancel out, leaving only the length scale of the tiny grooves. Simply put, the longer the tiny grating that generates the air pocket, the less the effect of the surfactant molecules.
It turns out there’s a critical air pocket length, which depends on the surfactant type and on its concentration. “If you make the grating longer, usually about 10 centimeters long, the surfactant can’t quite do its thing of resisting the fluid motion,” he said. “And you could get this ideal drag reduction that people have been angling for, for 20 years.”
With those calculations nicely resolved, the researchers will start looking at other types of SHS patterns, such as tiny posts, as well as other real-life situations such as turbulence and other unsteady flows. Being able to reduce drag in a variety of situations would result in more fuel-efficient cargo ships, more effective pumps and more resilient structures in flowing water.
More information:
Fernando Temprano-Coleto et al, A single parameter can predict surfactant impairment of superhydrophobic drag reduction, Proceedings of the National Academy of Sciences (2023). DOI: 10.1073/pnas.2211092120
Provided by
University of California – Santa Barbara
Citation:
Researchers find the key to reducing drag on superhydrophobic surfaces can come down to a single parameter (2023, February 2)