In math class, you probably learned how to compute the area of lots of different shapes by memorizing algebraic formulas. Remember “base x height” for rectangles and “½ base x height” for triangles? Or “𝜋 x radius²” for circles?
But if you were in math class in ancient Greece, you might have learned something very different. Ancient Greek mathematicians, such as Euclid, thought of area as something geometric, not algebraic. Euclid’s geometric perspective, recorded in his foundational work “Elements,” has influenced research programs across centuries – even the work of mathematicians today, like the two of us.
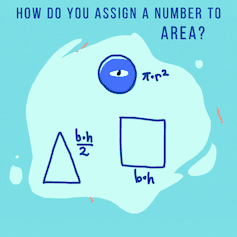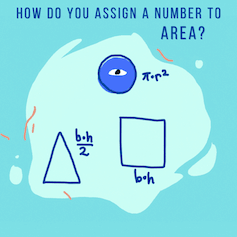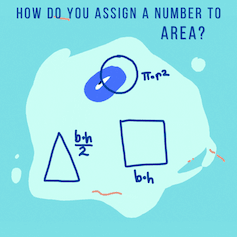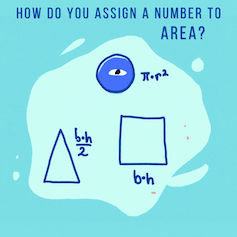
Math today treats area algebraically, using formulas for simple shapes and calculus for more complicated regions.
Maxine Calle, CC BY-ND
Modern mathematicians refer to Euclid’s concept of “having equal area” as “being scissors congruent.” This idea, based on cutting up shapes and pasting them back together in different ways, has inspired interesting mathematics beyond just computing areas of triangles and squares. The story of scissors congruence demonstrates how classical problems in geometry can find new life in the strange world of abstract modern math.
Euclid’s notion of area
Today, people think of the area of a shape as a single number that can be computed using algebraic formulas or calculus. So what does it mean to think of area as something geometric the way the ancient Greeks did?
Imagine you’re back in math class and you have a pair of scissors, some tape and a piece of construction paper. Your teacher instructs you to make a new flat, two-dimensional shape using all of the construction paper and only straight-line cuts. Using your scissors, you cut the paper into a bunch of pieces. You start moving these pieces around – maybe you rotate them or flip them over – and you tape them back together to form a new shape.

What kind of shapes can you make from a pentagon using only scissors and tape?
Maxine Calle, CC BY-ND
Using your algebraic formulas for area, you could check that the area of your new shape is equal to the original area of the construction paper. No matter how a 2D shape is cut up – as long as all the pieces are taped back together without overlap – the area of the old and the new shape will always be equal.

You’re not allowed to make curved cuts or tape overlapping pieces.
Maxine Calle, CC BY-ND
For Euclid, area is the measurement that is preserved by this geometric “cutting-and-pasting.” He would say that the new shape you made is “equal” to the original piece of construction paper – mathematicians today would say the two are “scissors congruent.”
What can your new shape look like? Because you’re only allowed to make straight-line cuts, it has to be a polygon, meaning none of the sides can be curved.




