You scrambled up a Rubik’s cube, and now you want to put it back in order. What sequence of moves should you make?
Surprise: You can answer this question with modern algebra.
Most folks who have been through high school mathematics courses will have taken a class called algebra – maybe even a sequence of classes called algebra I and algebra II that asked you to solve for x. The word “algebra” may evoke memories of complicated-looking polynomial equations like ax² + bx + c = 0 or plots of polynomial functions like y = ax² + bx + c.
You might remember learning about the quadratic formula to figure out the solutions to these equations and find where the plot crosses the x-axis, too.
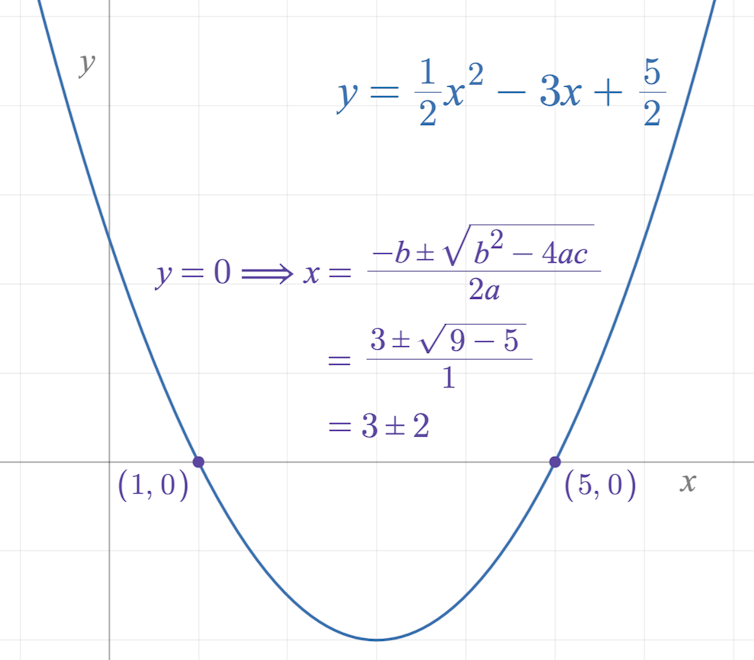
Graph of a quadratic equation and its roots via the quadratic formula.
Jacob Rus, CC BY-SA
Equations and plots like these are part of algebra, but they’re not the whole story. What unifies algebra is the practice of studying things – like the moves you can make on a Rubik’s cube or the numbers on a clock face you use to tell time – and the way they behave when you put them together in different ways. What happens when you string together the Rubik’s cube moves or add up numbers on a clock?
In my work as a mathematician, I’ve learned that many algebra questions come down to classifying objects by their similarities.
Sets and groups
How did equations like ax² + bx + c = 0 and their solutions lead to abstract algebra?
The short version of the story is that mathematicians found formulas that looked a lot like the quadratic formula for polynomial equations where the highest power of x was three or four. But they couldn’t do it for five. It took mathematician Évariste Galois and techniques he developed – now called group theory – to make a convincing argument that no such formula could exist for polynomials with a highest power of five or more.
So what is a group, anyway?
It starts with a set, which is a collection of things. The fruit bowl in my kitchen is a set, and the collection of things in it are pieces of fruit. The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 also form a set. Sets on their own don’t have too many properties – that is, characteristics – but if we start doing things to the numbers 1 through 12, or the fruit in the fruit bowl, it gets more interesting.
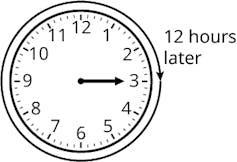
In clock addition, 3 + 12 = 3.
OpenStax, CC BY-SA
Let’s call this set of numbers 1 through 12 “clock numbers.” Then, we can define an addition function for the clock numbers using the way we tell time. That is, to say “3 + 11 = 2” is the way we would add 3 and 11. It feels weird, but if you think about it, 11 hours past 3 o’clock is 2 o’clock.
Clock addition has some nice properties. It satisfies:
closure, where adding things in the set gives you something else in the set,
identity, where there’s an element that doesn’t change the value of other…


