If you drop a light object and a heavy object from a tower, which one reaches the ground first? As you may recall from high school physics, this is a trick question. Neglecting air resistance, they both fall the same way and reach the ground at the same time – gravity means that their speeds increase at 9.8 meters per second squared, no matter what their mass.
That’s the premise behind Galileo Galilei’s Leaning Tower of Pisa experiment, a classic thought experiment in the field of dynamics.
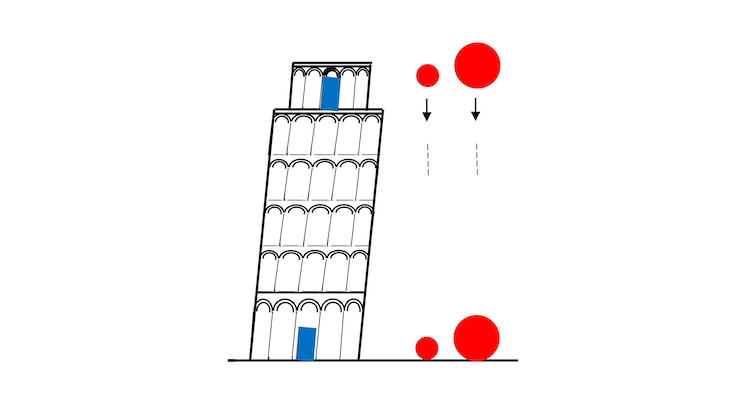
In the Leaning Tower of Pisa experiment, two spheres with different masses are dropped from a tower.
Larry M. Silverberg
Dynamics is the physics specialization that studies motion and force. A “dynamicist,” one who studies dynamics, can do everything from improve a basketball player’s free throw to help design spacecraft for interstellar travel.
As a dynamicist, I’ve spent much of my career helping students make sense of modern dynamics. The Leaning Tower of Pisa experiment is one good way to do this. It can explain how classical mechanics – the field that engineers and educators employ every day – was brought into the modern world.
Galileo’s Leaning Tower of Pisa experiment
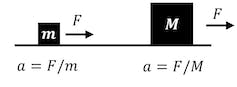
Two different blocks sliding on a surface, subject to the same applied interaction forces.
Larry M. Silverberg
The Leaning Tower of Pisa experiment led to the curious realization that objects fall with the same accelerations regardless of their mass. But what happens when you place objects of different masses on a smooth table and push each of them with the same force?
Even without accounting for friction, the objects’ accelerations are now different. The lighter objects accelerate more than the heavy ones. When falling, their accelerations are the same, yet when sliding, they’re different.
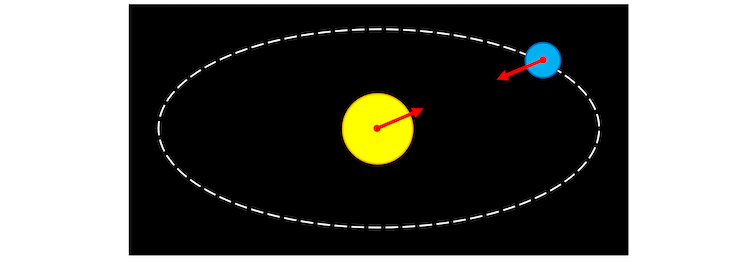
In modern mechanics, we recognize that the magnitudes of the action forces by the Sun and the Earth are in proportion to their respective gravitational masses.
Larry M. Silverberg
Let’s now place the two objects in orbit. Imagine one of them is the Sun and the other is the Earth. In classical mechanics, the Sun exerts a force on the Earth equal in magnitude to the force that the Earth exerts back on the Sun.
But the Sun is huge compared with the Earth. Shouldn’t the magnitude of the larger object’s force be larger? And while we’re at it, how would the magnitude of the Sun’s force on the Earth come to be equal to the magnitude of the Earth’s force on the Sun?
Heavy and light objects have equal accelerations when falling but different accelerations when sliding, and objects in space exert equal gravitational forces on each other despite having different masses. This all seems inconsistent, and a little confusing, right?
Modern mechanics
The problems above came from an ambiguity in the concept of force in classical mechanics. In…



