Solving the equations of general relativity for colliding black holes is no simple matter.
Physicists began using supercomputers to obtain solutions to this famously hard problem back in the 1960s. In 2000, with no solutions in sight, Kip Thorne, 2018 Nobel Laureate and one of the designers of LIGO, famously bet that there would be an observation of gravitational waves before a numerical solution was reached.
He lost that bet when, in 2005, Carlos Lousto, then at The University of Texas at Brownsville, and his team generated a solution using the Lonestar supercomputer at the Texas Advanced Computing Center. (Concurrently, groups at NASA and Caltech derived independent solutions.)
In 2015, when the Laser Interferometer Gravitational-Wave Observatory (LIGO) first observed such waves, Lousto was in shock.
“It took us two weeks to realize this was really from nature and not from inputting our simulation as a test,” said Lousto, now a professor of mathematics at Rochester Institute of Technology (RIT). “The comparison with our simulations was so obvious. You could see with your bare eyes that it was the merger of two black holes.”
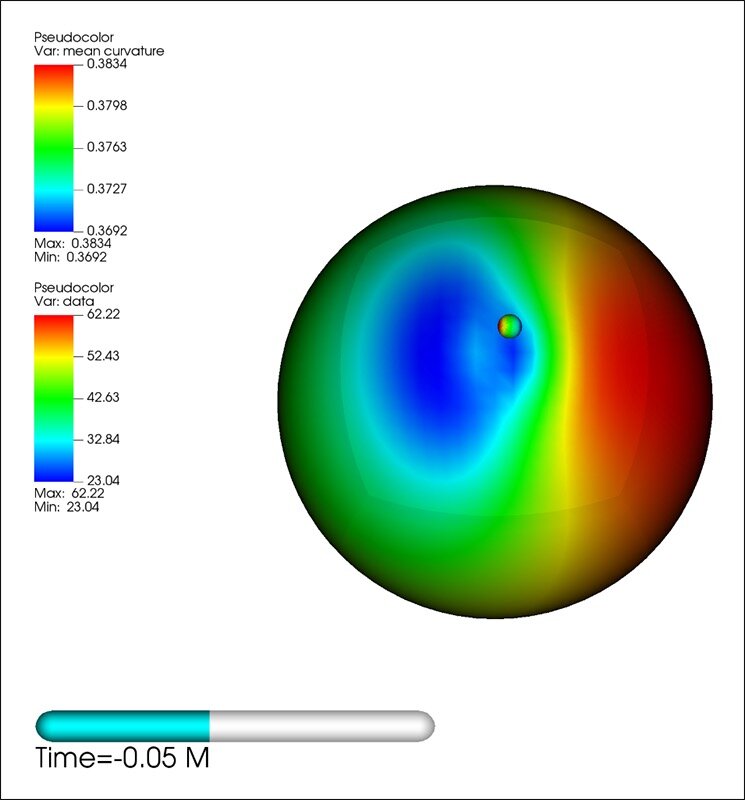
Lousto is back again with a new numerical relativity milestone, this time simulating merging black holes where the ratio of the mass of the larger black hole to the smaller one is 128 to 1—a scientific problem at the very limit of what is computational possible. His secret weapon: the Frontera supercomputer at TACC, the eighth most powerful supercomputer in the world and the fastest at any university.
His research with collaborator James Healy, supported by the National Science Foundation (NSF), was published in Physical Review Letters [journals.aps.org/prl/abstract/ … ysRevLett.125.191102] this week. It may require decades to confirm the results experimentally, but nonetheless it serves as a computational achievement that will help drive the field of astrophysics forward.
“Modeling pairs of black holes with very different masses is very computational demanding because of the need to maintain accuracy in a wide range of grid resolutions,” said Pedro Marronetti, program director for gravitational physics at NSF. “The RIT group has performed the world’s most advanced simulations in this area, and each of them takes us closer to understanding observations that gravitational-wave detectors will provide in the near future.”
LIGO is only able to detect gravitational waves caused by small and intermediate mass black holes of roughly equal size. It will take observatories 100 times more sensitive to detect the type of mergers Lousto and Healy have modeled. Their findings show not only what the gravitational waves caused by a 128:1 merger would look like to an observer on Earth, but also characteristics of the ultimate merged black hole including its final mass, spin, and recoil velocity. These led to some surprises.
“These merged black holes can have speeds much larger than previously known,” Lousto said. “They can travel at 5,000 kilometers per second. They kick out from a galaxy and wander around the universe. That’s another interesting prediction.”
The researchers also computed the gravitational waveforms—the signal that would be perceived near Earth—for such mergers, including their peak frequency, amplitude, and luminosity. Comparing those values with predictions from existing scientific models, their simulations were within 2 percent of the expected results.
Previously, the largest mass ratio that had ever been solved with high-precision was 16 to 1—eight times less extreme than Lousto’s simulation. The challenge of simulating larger mass ratios is that it requires resolving the dynamics of the interacting systems at additional scales.
Like computer models in many fields, Lousto uses a method called adaptive mesh refinement to get precise models of the dynamics of the interacting black holes. It involves putting the black holes, the space between them, and the distant observer (us) on a grid or mesh, and refining the areas of the mesh with greater detail where it is needed.
Lousto’s team approached the problem with a methodology that he compares to Zeno’s first paradox. By halving and halving the mass ratio while adding internal grid refinement levels, they were able to go from 32:1 black hole mass ratios to 128:1 binary systems that undergo 13 orbits before merger. On Frontera, it required seven months of constant computation.
“Frontera was the perfect tool for the job,” Lousto said. “Our problem requires high performance processors, communication, and memory, and Frontera has all three.”
The simulation isn’t the end of the road. Black holes can have a variety of spins and configurations, which impact the amplitude and frequency of the gravitational waves their merger produces. Lousto would like to solve the equations 11 more times to get a good first range of possible “templates” to compare with future detections.
The results will help the designers of future Earth- and space-based gravitational wave detectors plan their instruments. These include advanced, third generation ground based gravitational wave detectors and the Laser Interferometer Space Antenna (LISA), which is targeted for launch in the mid-2030s.
The research may also help answer fundamental mysteries about black holes, such as how some can grow so big—millions of times the mass of the Sun.
“Supercomputers help us answer these questions,” Lousto said. “And the problems inspire new research and pass the torch to the next generation of students.”
Researchers reveal the origins of merging black holes
More information:
Carlos O. Lousto et al, Exploring the Small Mass Ratio Binary Black Hole Merger via Zeno’s Dichotomy Approach, Physical Review Letters (2020). DOI: 10.1103/PhysRevLett.125.191102
Provided by
University of Texas at Austin
Citation:
Final dance of unequal black hole partners (2020, November 6)
retrieved 8 November 2020
from https://phys.org/news/2020-11-unequal-black-hole-partners.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no
part may be reproduced without the written permission. The content is provided for information purposes only.