Humans are very good at spotting patterns, or repeating features people can recognize. For instance, ancient Polynesians navigated across the Pacific by recognizing many patterns, from the stars’ constellations to more subtle ones such as the directions and sizes of ocean swells.
Very recently, mathematicians like me have started to study large collections of objects that have no patterns of a particular sort. How large can collections be before a specified pattern has to appear somewhere in the collection? Understanding such scenarios can have significant real-world implications: For example, what’s the smallest number of server failures that would lead to the severing of the internet?
Research from mathematician Jordan Ellenberg at the University of Wisconsin and researchers at Google’s Deep Mind have proposed a novel approach to this problem. Their work uses artificial intelligence to find large collections that don’t contain a specified pattern, which can help us understand some worst-case scenarios.
Patterns in the card game Set
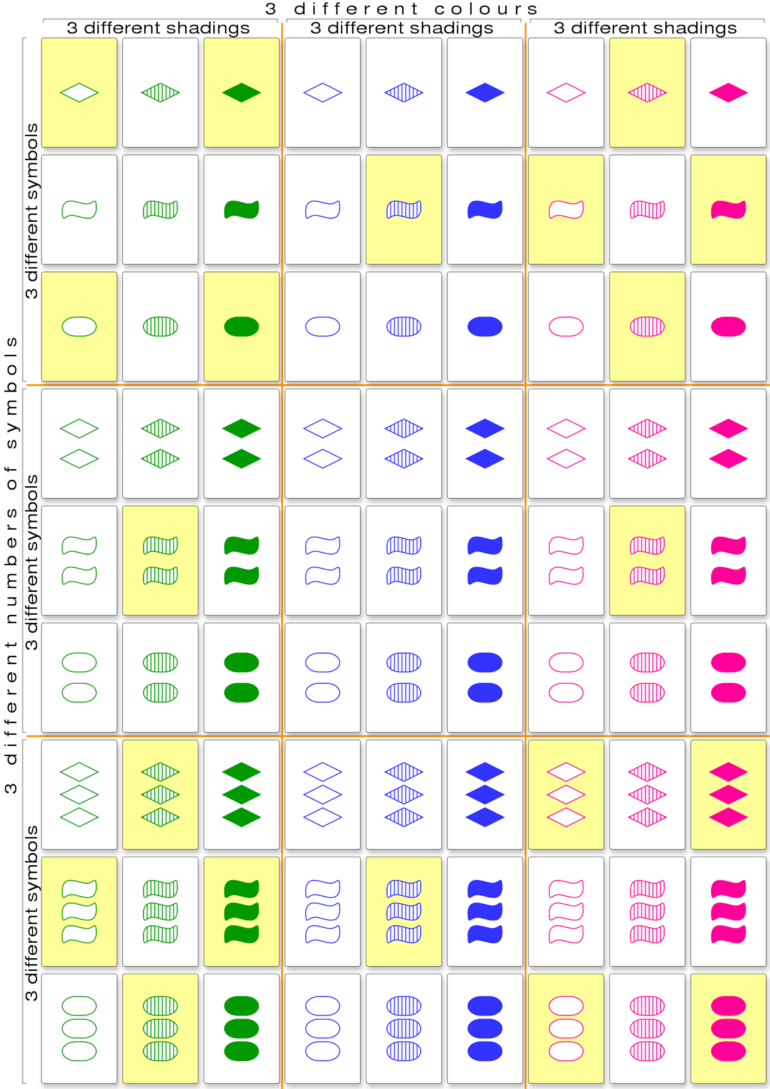
The idea of patternless collections can be illustrated by a popular card game called Set. In this game, players lay out 12 cards, face up. Each card has a different simple picture on it. They vary in terms of number, color, shape and shading. Each of these four features can have one of three values.
Players race to look for “sets,” which are groups of three cards in which every feature is either the same or different in each card. For instance, cards with one solid red diamond, two solid green diamonds and three solid purple diamonds form a set: All three have different numbers (one, two, three), the same shading (solid), different colors (red, green, purple) and the same shape (diamond).
Marsha Falco originally created the game Set to help explain her research on population genetics.
Finding a set is usually possible – but not always. If none of the players can find a set from the 12 cards on the table, then they flip over three more cards. But they still might not be able to find a set in these 15 cards. The players continue to flip over cards, three at a time, until someone spots a set.
So what is the maximum number of cards you can lay out without forming a set?
In 1971, mathematician Giuseppe Pellegrino showed that the largest collection of cards without a set is 20. But if you chose 20 cards at random, “no set” would happen only about one in a trillion times. And finding these “no set” collections is an extremely hard problem to solve.
Finding ‘no set’ with AI
If you wanted to find the smallest collection of cards with no set, you could in principle do an exhaustive search of every possible collection of cards chosen from the deck of 81 cards. But there are an enormous number of possibilities – on the order of 1024 (that’s a “1” followed by 24 zeros). And if you increase the number of…