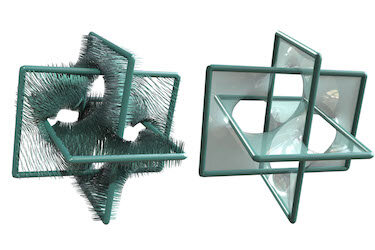
Consider a soap bubble. The way it contains the minimal possible surface area is surprisingly efficient. This is not a trivial issue. Mathematicians have been looking for better ways to calculate minimal surfaces for hundreds of years. Recently, Computer Science and Engineering Department Assistant Professor Albert Chern, and postdoctoral researcher Stephanie Wang, added a new page to this book with their paper: Computing Minimal Surfaces with Differential Forms, which was recently published by ACM Transactions on Graphics.
“Other than modeling soap films, these shapes are the foundation for many micro structures, such as in tissues in biology,” said Chern. “If you zoom into bone structures, you’ll see these membranes that tend to form minimal surfaces. Basically, the surface tension on either side of the membrane is canceling itself out.”
These measurements can also be applied to architecture. Chern points to the Olympic Park in Munich, which was inspired by minimal surfaces. Regardless of the application, finding the most efficient method to determine minimal surfaces is a valuable proposition.
Plateau’s problem
Calculating a minimal surface within a boundary curve—the path around its edge—is called Plateau’s problem, after Joseph Plateau, who was born in 1801 and liked to experiment with soap bubbles. As new technologies have emerged, our ability to solve for minimal surfaces has slowly improved. Most recently, mathematicians have used an old approach called gradient descent (not to be confused with the machine learning algorithm), which until recently was state of the art.
Oddly enough, Chern got into this area, to some degree, because of ants. “I was looking at optimal transport problems,” says Chern. “Let’s say you have an ant hill and a little ways away you have a pile of food. What is the optimal path for the ants to take to get that food and bring it back to their anthill?”
In real life, ants can’t do the math, but they have still figured out the problem, creating optimal paths to food sources. No doubt, this ability evolved as a survival mechanism to gain the greatest nutritional benefit at the least metabolic cost. Chern saw the similarities between this optimal transport problem and minimal surfaces and, in a sense, combined them.
One of the advantages of Chern’s new method is that it doesn’t care about variations in a shape’s topology. Previous methods, such as using triangle mesh, required different approaches based on topology. As a result, handling varied surface topologies has become much easier.
“It’s a completely different approach to looking at minimal surface problems—generalizing this interesting optimal transport problem,” said Chern. “And then it suddenly becomes this big, well-known mathematical problem and that gives it a very different flavor.”
More information:
Stephanie Wang et al, Computing minimal surfaces with differential forms, ACM Transactions on Graphics (2021). DOI: 10.1145/3450626.3459781
Provided by
University of California – San Diego
Citation:
A brief history of minimal surfaces and the ants that love them (2021, November 17)