Mathematicians at The University of Manchester have answered the question: How many lottery tickets do you need to buy to guarantee wining something on the U.K. National Lottery?
Focusing on the National Lottery’s flagship game “Lotto,” which draws six random numbers from 1 to 59, Dr. David Stewart and Dr. David Cushing found that 27 is the lowest possible number of tickets needed to guarantee a win—although, importantly, with no guarantee of a profit.
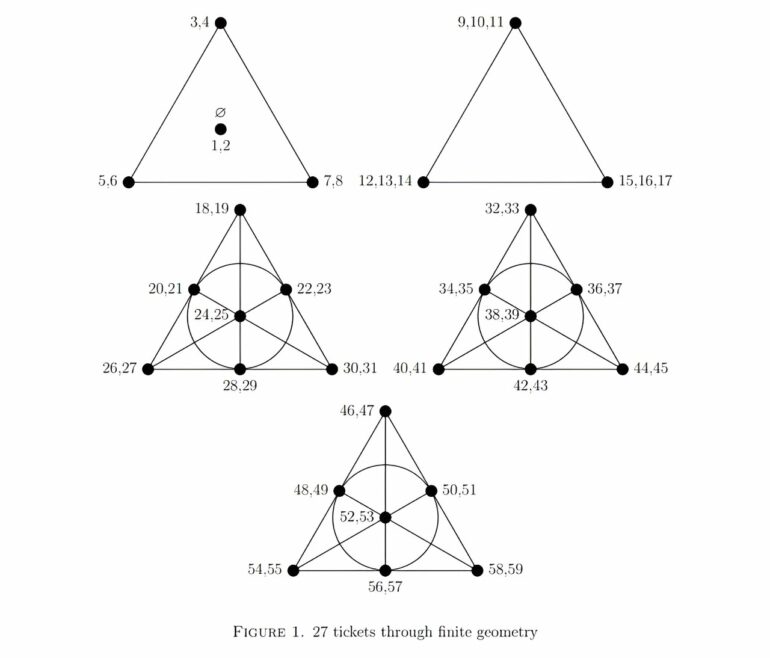
They describe the solution using a mathematical system called finite geometry, which centers around a triangle-like structure called a Fano plane. Each point of the structure is plotted with pairs of numbers and connected with lines—each line generates a set of six numbers, which equates to one ticket.
It takes three Fano planes and two triangles to cover all 59 numbers and generate 27 sets of tickets.
Choosing tickets in this way guarantees that no matter which of the 45,057,474 possible draws occurs, at least one of the tickets will have at least two numbers in common. From any draw of six, two numbers must appear on one of the five geometric structures, which ensures they appear on at least one ticket.
But Dr. Stewart and Dr. Cushing say that the hard work is actually showing that achieving the same outcome with 26 tickets is not possible.

The 27 sets of lottery ticket numbers. © University of Manchester
Dr. David Stewart, a Reader in Pure Mathematics at The University of Manchester, said, “Fundamentally there is a tension which comes from the fact that there are only 156 entries on 26 tickets. This means a lot of numbers can’t appear a lot of times. Eventually you see that you’ll be able to find six numbers that don’t appear on any ticket together. In graph theory terms, we end up proving the existence of an independent set of size six.”
Although guaranteed a win, the researchers say that the chances of making a profit are very unlikely and shouldn’t be used as a reason to gamble.
The 27 lottery tickets would set you back £54. And Peter Rowlett, a mathematician from The Aperiodical website, has shown that in almost 99% of cases, you wouldn’t make that money back.
When putting the theory to the test in the lottery draw on 1 July 2023; the researchers matched just two balls on three of the tickets, the reward being three lucky dip tries on a subsequent lottery, each of which came to nothing.
The researchers say that the finding is interesting from a computational point of view. They use a fifty-year-old programming language called Prolog, which they say makes it one of the oldest examples of real artificial intelligence.
Provided by
University of Manchester
Citation:
How many lottery tickets do you need to buy to guarantee a win? Mathematicians find the answer (2023, August 3)