Have you ever wondered about the best way to pack a finite number of identical spheres into a shape-shifting flexible container, like a convex hull?
Researchers from the University of Twente, Active Soft Matter Lab led by Dr. Hanumantha Rao Vutukuri in the TNW Faculty, along with Utrecht University, have investigated this fascinating mathematical sphere-packing problem by combining experiments and computer simulations. Their research has been published in Nature Communications.
An intuitively simple problem concerning the best way to pack a set of spheres has a long history of studies dating back to the 17th century. The British sailor Raleigh, for instance, contemplated this issue while trying to find an efficient method for stacking cannonballs on his ship.
Later, Kepler conjectured that the densest packing for an infinite number of spheres would be the face-centered cubic (FCC) crystal structure, akin to the hexagonal arrangement of oranges and apples seen in supermarkets. Remarkably, this hypothesis was only proven in the 21st century.
The ‘sausage catastrophe’
When you have a finite number of spheres, everything gets more complicated; surprisingly, packing the “finite” spheres in a compact cluster does not always yield the densest packing. Mathematicians already conjectured decades ago that a linear, sausage-like arrangement provides the best packing, however, not for all numbers of spheres.
There’s a peculiar phenomenon at play: The sausage-shaped arrangement is the most efficient packing, but only with up to 55 spheres. Beyond that number, a clustered arrangement becomes the best packing. This abrupt transition is known as the “sausage catastrophe.”
In three-dimensional space, packing up to 55 spheres linearly forms a “sausage” that is denser than any cluster arrangement. However, in four dimensions, this scenario changes dramatically. About 300,000 spheres are needed for the “sausage” to transform into a spherelike cluster.
Rao was curious about whether this fundamentally intriguing problem could be observed and resolved in the lab using a model system. This system includes micron-sized spherical particles (colloids) and giant unilamellar vesicles (GUVs), which serve as flexible containers that are the main ingredients in Vutukuri’s lab.
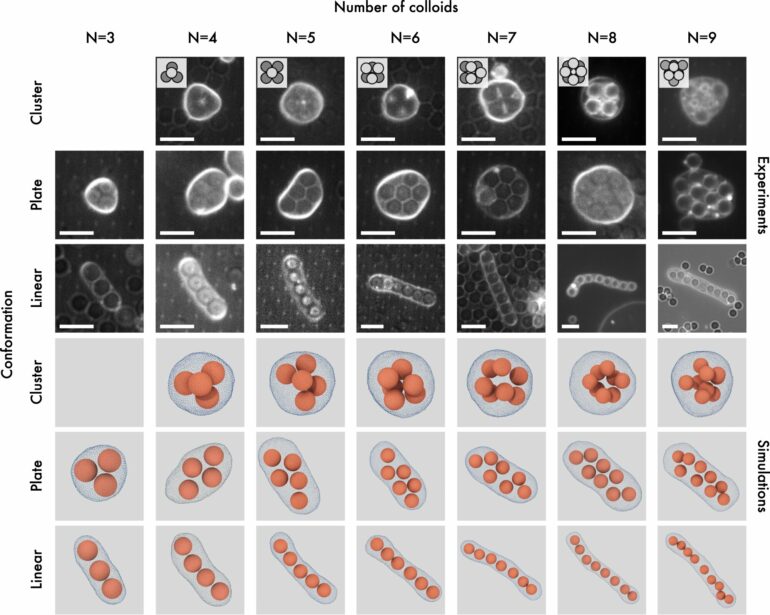
“This curiosity led us to explore the finite sphere packing problem through experiments in 3D real space, specifically using colloids in GUVs. By varying the number of particles and the volume of the vesicles, we were able to examine the different particle arrangements inside these vesicles using a confocal microscope.
“We identified stable arrangements for specific combinations of vesicle volume and particle number: 1D (sausage), 2D (plate, with particles in one plane), and 3D (cluster). Notably, we also observed bistability; the configurations alternated between 1D and 2D arrangements or between 2D and 3D structures. However, our experiments were limited to observing a maximum of nine particles, as packing a larger number of particles resulted in the rupture of the vesicles.”
Vutukuri says that they then contacted Dijkstra’s lab at Utrecht University to delve deeper into this problem using simulations. Strikingly, the simulations predicted that packing spheres in a sausage configuration is most efficient for up to 55 spheres. However, when they attempted to pack 56 spheres into a vesicle, they discovered that a compact three-dimensional cluster was the more efficient arrangement.
Remarkably, for 57 spheres, the packing reverted back to a sausage configuration. While mathematicians have previously determined that a sausage configuration is the most efficient for 58 and 64 spheres, their study contradicts this, demonstrating that compact clusters are more effective.
The findings show that the “sausage catastrophe,” a phenomenon previously described by mathematicians, is not just a theoretical scenario but can also be observed experimentally.
More information:
Susana Marín-Aguilar et al, A colloidal viewpoint on the sausage catastrophe and the finite sphere packing problem, Nature Communications (2023). DOI: 10.1038/s41467-023-43722-0
Provided by
University of Twente
Citation:
Researchers use simulations to tackle finite sphere-packing problem and ‘sausage catastrophe’ (2024, January 31)