We often crumple a scrap piece of paper into a ball before throwing it. This mundane action, however, creates a unique complex system with surprising mechanical properties. Take a thin plastic sheet such as cellophane and try it yourself. While a regular flat sheet will simply bend under the influence of gravity, a crumpled sheet is stiffer and can hold its own weight. It also has shape memory—it has many stable configurations and thus will tend to keep the shape it is deformed to.
Dr. Yoav Lahini from Tel Aviv University has long been obsessed with crumpled thin sheets. “This is far from a curiosity,” he explains. “Crumpled sheets share many of their strange behaviors with a wide range of other complex systems that are harder to study. The ability to hold the experiment in your hand can bring so much intuition.”
In a new study published in Nature Physics, Dr. Lahini and his students Dor Shohat and Yaniv Friedman use crumpled sheets to shed new light on the mechanism underlying slow relaxations and physical aging, a long-standing question in the physics of disordered systems.
The never-ending relaxation
To understand the problem, consider the following tabletop experiment: Take a thin sheet, crumple it into a ball and place it under a weight. Instead of relaxing to some fixed volume as one would expect, the crumpled ball will continue compacting under the weight without ever reaching equilibrium.
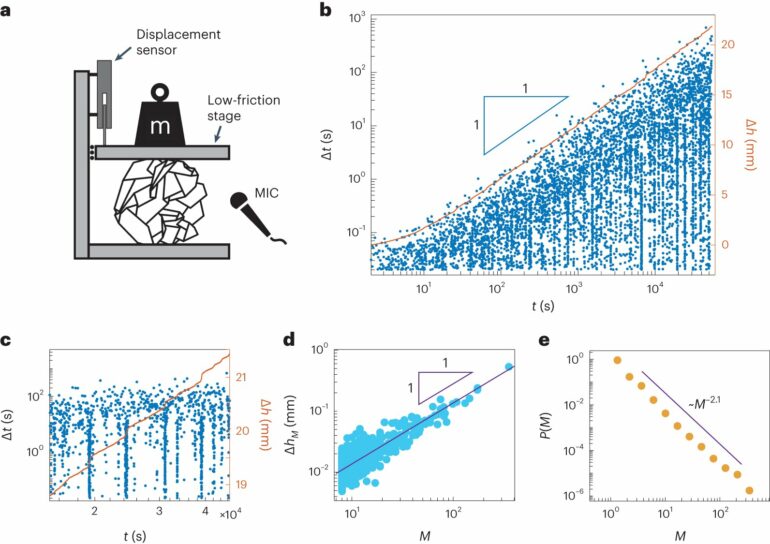
More than 20 years ago, experiments by Kittiwit Matan and colleagues have shown that this slow compaction is logarithmic in time, meaning the compaction rate keeps slowing down, but does not show signs of stopping even after several weeks.
Logarithmic relaxations are not unique to crumpled sheets. They appear across condensed matter physics in various disordered systems, from polymers and sandpiles to disordered conductors and glass, yet their microscopic origins are poorly understood.
Crumpled sheets offer experimental access that other systems do not. During the logarithmic relaxation, the crumpled sheet emits noise: intermittent crackling sounds, which originate from localized instabilities—small, bi-stable regions that snap through the sheet to release stress. The team realized that these snap-trough instabilities dictate the mechanical response of the sheet. The slow logarithmic relaxation is in fact intermittent and occurs via a sequence of abrupt instabilities.
The statistics of the acoustic emissions revealed an even more surprising result. Instabilities in the crumpled ball do not occur at random. In fact, they trigger one another, forming scale-free avalanches of instabilities. “This scenario resembles self-organized criticality, where the system spontaneously positions itself on the edge of stability, and avalanches of all sizes appear without any typical scale,” explains Shohat.
“But there’s a twist. The system evolves while exhibiting these critical avalanches. The avalanches correspond to a fixed, wide distribution, but they span more timescales and become more sparse as the system relaxes.”
A simplified model
To gain further insight into the relaxation mechanism, the researchers employed numerical simulations of a disordered elastic network that represents the sheet. In the model, each bond in the network is bi-stable, essentially an elastic spring but with two rest lengths. This represents the localized instabilities observed experimentally. Under external forcing, the simulated network compacted intermittently via abrupt, scale-free and slowing avalanches, capturing all experimental observations.
The simulations revealed that the slowing logarithmic relaxation is driven by a simple mechanism: before each compaction step, one of the bonds is positioned on the verge of instability, close to snapping between its rest lengths. The snapping is activated by noise in a stochastic process, triggering an avalanche of instabilities.
After each avalanche, the energy barrier to trigger the next instability slightly increases, resulting in a longer crossing time. The increase waiting times between avalanches results in the slowdown of the dynamics and generically leads to a logarithmic relaxation.
Lahini says, “The simplicity of the mechanism suggests that it can be relevant to a range of disordered systems. Searching for similar signature of intermittent relaxations composed of slowing avalanches could help understand the dynamics of glassy systems, amorphous solids and even earthquakes.”
More information:
Dor Shohat et al, Logarithmic aging via instability cascades in disordered systems, Nature Physics (2023). DOI: 10.1038/s41567-023-02220-2
Provided by
Tel Aviv University
Citation:
Crumpled sheets reveal a mechanism for glassy relaxations (2023, November 8)