Scientists have used computational algebraic geometry to study predictions for particle physics experiments, such as those at the Large Hadron Collider (LHC), which first detected the Higgs particle in 2012.
These experiments, in combination with new mathematical tools, help to solve unanswered questions in physics in a much faster way and have a profound impact on our understanding of nature. The team’s results were published in Physical Review Letters in March. The research team includes Sebastian Mizera, a member of the School of Natural Sciences, and his collaborators Claudia Fevola (Université Paris-Saclay, Inria) and Simon Telen (Max Planck Institute for Mathematics in the Sciences),
“Our progress was made possible by utilizing recently-developed tools in computational algebraic geometry,” said Mizera, who is concluding his five-year term at IAS this summer. “It’s a rare example where using cutting-edge tools from mathematics has a direct impact on practical computations in particle physics.”
When studying particle collisions, physicists seek to describe the probability of particles arriving at certain states: whether they pass through each other, transform, or scatter at different angles, for example. This allows them to identify new particles or classify characteristics of existing ones. In order to do this, they must study particle interactions at the quantum level.
However, in quantum theory, it is impossible to predict the outcomes of particle collision with total certainty. Instead, physicists compute “scattering amplitudes,” which are mathematical expressions that encode the likelihood of different possible outcomes occurring when particles interact or collide. One of the characteristic features that physicists look for in these amplitudes are their “singularities,” which are points or regions where the probability amplitudes become infinite or undefined.
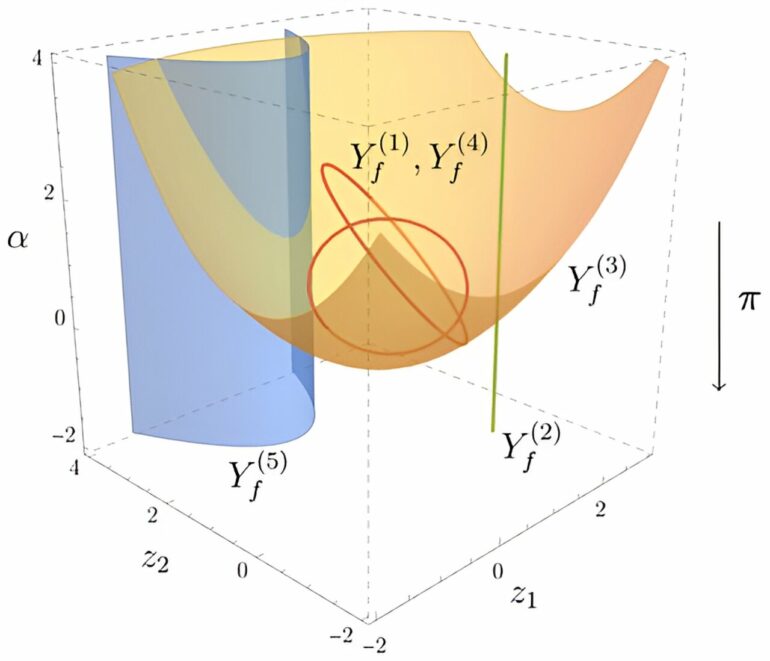
In their paper, Mizera and his colleagues used mathematical tools including topology, geometry, and algebra to better understand a particular kind of singularity, namely Landau singularities. Landau singularities are geometric objects that quantify when virtual particles (those limited by the uncertainty principle) become observable particles.
By understanding the implications of Landau singularities, physicists can identify the energy scales and kinematic regimes where new phenomena, such as the production of new particles, may become possible. This plays an important role in interpreting and making predictions for experiments.
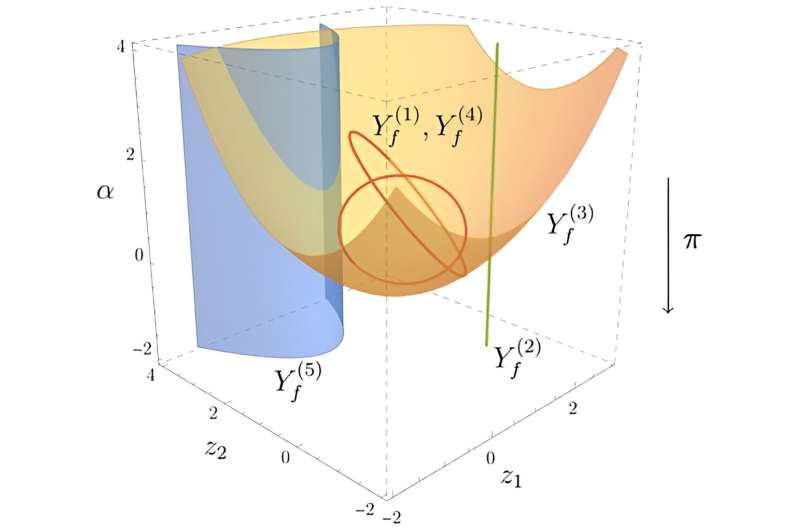
A representation of Landau singularities, described by algebraic equations. © Institute for Advanced Study
An algebraic variety called the “principal Landau determinant,” introduced by Mizera and his collaborators in their paper, is likely to be even more helpful in this regard. The principal Landau variant finds singularities even in the presence of massless particles.
This is significant: locating singularities in the presence of massless particles is simultaneously the case most important to understanding the physics of the LHC and the most difficult to compute from a mathematical perspective.
This ability was demonstrated in the paper with a number of examples, including calculations needed to understand Higgs boson production in the presence of strong nuclear forces.
It is a major step in the ongoing progress by physicists worldwide to increase the high-precision computational capability used to verify predictions of the Standard Model of particle physics at the LHC. Theoretical physicists like Mizera and his collaborators are an essential piece of this particle puzzle.
More information:
Claudia Fevola et al, Landau Singularities Revisited: Computational Algebraic Geometry for Feynman Integrals, Physical Review Letters (2024). DOI: 10.1103/PhysRevLett.132.101601
Provided by
Institute for Advanced Study
Citation:
Cutting-edge mathematics provides new tool for particle collision puzzle (2024, June 7)