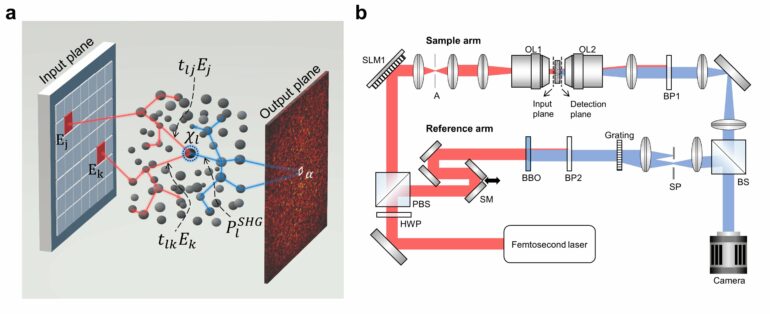
Can one see through a scattering medium like ground glass? Conventionally, such a feat would be deemed impossible. As light travels through an opaque medium, the information contained in the light becomes “jumbled up,” almost as if undergoes complex encryption. Recently, Professor Choi Wonshik’s team from the IBS Center for Molecular Spectroscopy and Dynamics (IBS CMSD) has discovered a way to utilize this phenomenon in optical computing and machine learning.
Since 2010, several previous studies have attempted to harness information lost due to scattering media, such as biological tissues, using mathematics. This has been typically done by employing optical operators such as linear scattering matrices, which can be used to determine the input-output relationships of photons as they undergo scattering.
This topic has been of primary research interest for Professor Choi’s team from the IBS CMSD, and they have published many works that combine both hardware- and software-based adaptive optics for tissue imaging. Some of their work was demonstrated in new types of microscopes that can see through scattering media with high opacity, such as mouse skulls, as well as perform deep 3D-imaging of tissues.
However, things become much more complex when nonlinearity enters the equation. If a scattering medium generates nonlinear signals, it can no longer be represented simply by a linear matrix, as the principle of superposition is violated. Moreover, measuring the nonlinear input-output characteristics becomes a daunting challenge, setting a demanding stage for research.
Unraveling the mystery of nonlinear scattering media
This time, Professor Choi’s team has achieved yet another scientific breakthrough. They became the first to discover that the optical input-output response of a nonlinear scattering medium can be defined by a third-order tensor, as opposed to a linear matrix. The findings are published in the journal Nature Physics.
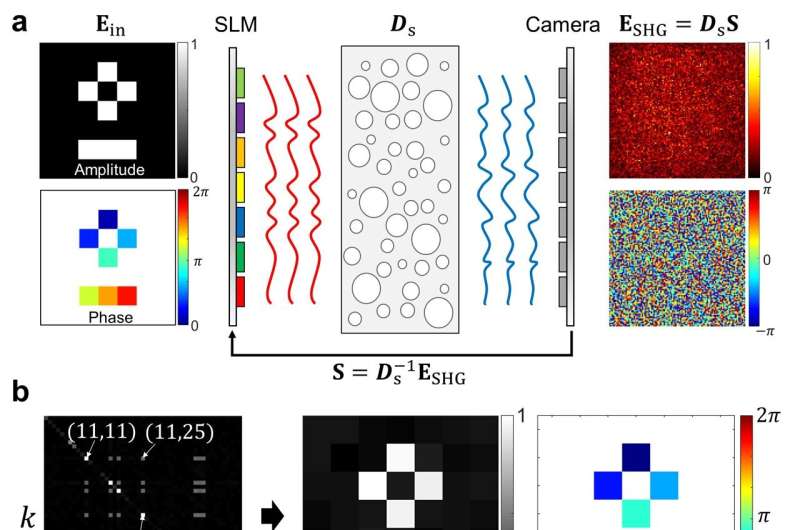
Nonlinear optical encryption using tensor. The information of light that is scattered and modulated by the nonlinear scattering medium randomly changes, making it difficult to reconstruct the original information, as shown in the right image of (a). This can be referred to as optical encryption. However, by knowing the input-output response characteristics, it is possible to reconstruct the original information from the random output speckle, as shown in (b). This process can be considered as decrypting the encrypted information. With only linear response characteristics that do not involve cross-terms, it was not possible to correctly reconstruct the information, as shown in (c). © Institute for Basic Science
Third-order tensor is a mathematical object used to represent relationships between three sets of data. In simple terms, it is an array of numbers arranged in a three-dimensional structure. Tensors are generalizations of scalars (0-order tensors), vectors (1st-order tensors), and matrices (2nd-order tensors) and are commonly used in various fields of mathematics, physics, and engineering to describe physical quantities and their relationships.
To demonstrate this, the team utilized a medium comprised of barium titanate nanoparticles, which generate nonlinear second harmonic generation (SHG) signals due to the inherent noncentrosymmetric properties of barium titanate. These SHG signals emerge as a square of the input electric field through the second harmonic process, causing cross-terms when multiple input channels are activated simultaneously, disrupting the linear superposition principle. The researchers devised and experimentally validated a novel theoretical framework involving these cross-terms in a 3rd-order tensor.
To illustrate this, the researchers measured cross-terms by isolating the difference between the output electric fields produced when two input channels were activated simultaneously, and when each channel was activated separately. This necessitated an additional 1,176 measurements set by the possible combinations of two independent input channels, even with just 49 input channels.
“The effort required to detect cross-terms from weak nonlinear signals was significant,” noted Dr. Moon Jungho, the study’s lead author.
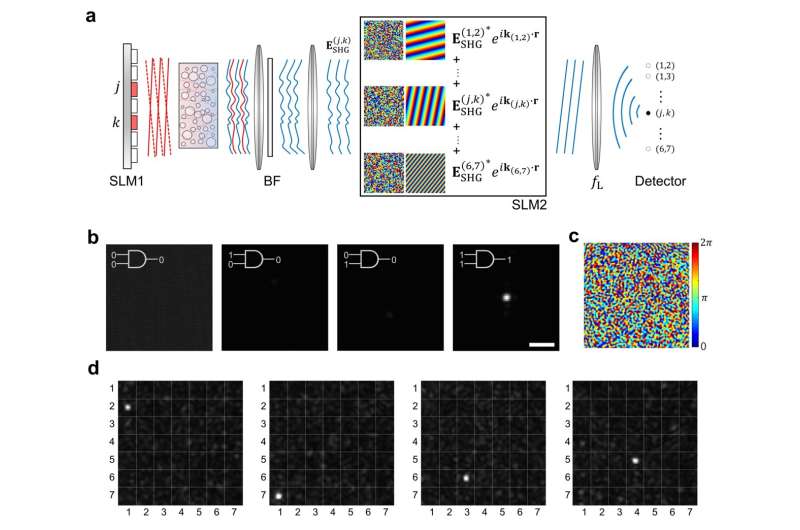
Nonlinear all-optical logic circuit. (a) A nonlinear optical logic circuit was implemented using the digital phase-conjugation method with a nonlinear scattering medium. By utilizing the phase-conjugate field of the cross-term (c), it is possible to create an AND gate (b) that focuses light only when both input channels are active at the same time. Since all nonlinear input-output responses are recorded, it is also possible to implement a multi-channel AND gate as shown in (d). © Institute for Basic Science
Real-world applications unleashed
The tensor derived from the nonlinear scattering medium has a higher rank than matrices of linear scattering media, hinting at its potential as a scalable physical operator. The team demonstrated this through the real-world implementation of nonlinear optical encryption and all-optical logic gates.
First, the team successfully demonstrated that nonlinear scattering media can be used for the optical encryption process. When specific image information is input into the media, the output second harmonic wave signals are displayed as random patterns, akin to a series of encryption processes. Conversely, by performing an inverse operation of the 3rd-order tensor representation of the second harmonic wave, the original input information can be