Is nature really as strange as quantum theory says—or are there simpler explanations? Neutron measurements at TU Wien prove that it doesn’t work without the strange properties of quantum theory.
Can a particle be in two different places at the same time? In quantum physics, it can: Quantum theory allows objects to be in different states at the same time—or more precisely: in a superposition state, combining different observable states. But is this really the case? Perhaps the particle is actually in a very specific state, at a very specific location, but we just don’t know it?
The question of whether the behavior of quantum objects could perhaps be described by a simple, more classical theory has been discussed for decades. In 1985, a way of measuring this was proposed: the so-called “Leggett-Garg inequality.” Any theory that describes our world without the strange superposition states of quantum theory must obey this inequality.
Quantum theory, on the other hand, violates it. Measurements with neutrons testing this “Leggett-Garg inequality” have now been carried out for the first time at TU Wien—with a clear result: the Leggett-Garg inequality is violated, classical explanations are not possible, quantum theory wins. The results have now been published in the journal Physical Review Letters.
Physical realism
We normally assume that every object has certain properties: A ball is at a certain location, it has a certain speed, perhaps also a certain rotation. It doesn’t matter whether we observe the ball or not. It has these properties quite objectively and independently of us. “This view is known as ‘realism,'” says Stephan Sponar from the Atomic Institute at TU Wien.
We know from our everyday experience that large, macroscopic objects in particular must obey this rule. We also know that macroscopic objects can be observed without being influenced significantly. The measurement does not fundamentally change the state. These assumptions are collectively referred to as “macroscopic realism.”
However, quantum theory as we know it today is a theory that violates this macroscopic realism. If different states are possible for a quantum particle, for example different positions, speeds or energy values, then any combination of these states is also possible. At least as long as this state is not measured. During a measurement, the superposition state is destroyed: the measurement forces the particle to decide in favor of one of the possible values.
The Leggett-Garg inequality
Nevertheless, the quantum world must be logically connected to the macroscopic world—after all, large things are made up of small quantum particles. In principle, the rules of quantum theory should apply to everything.
So the question is: Is it possible to observe behavior in “large” objects that cannot be reconciled with our intuitive picture of macroscopic realism? Can macroscopic things also show clear signs of quantum properties?
In 1985, physicists Anthony James Leggett and Anupam Garg published a formula with which macroscopic realism can be tested: The Leggett-Garg Inequality.
“The idea behind it is similar to the more famous Bell’s inequality, for which the Nobel Prize in Physics was awarded in 2022,” says Elisabeth Kreuzgruber, first author of the paper.
“However, Bell’s inequality is about the question of how strongly the behavior of a particle is related to another quantum entangled particle. The Leggett-Garg inequality is only about one single object and asks the question: how its state at specific points in time related to the state of the same object at other specific points in time?”
Stronger correlations than classical physics allows
Leggett and Garg assumed an object that can be measured at three different times, each measurement can have two different results. Even if we know nothing at all about whether or how the state of this object changes over time, we can still statistically analyze how strongly the results at different points in time correlate with each other.
It can be shown mathematically that the strength of these correlations can never exceed a certain level—assuming that macroscopic realism is correct. Leggett and Garg were able to establish an inequality that must always be fulfilled by every macroscopic realistic theory, regardless of any details of the theory.
However, if the object adheres to the rules of quantum theory, then there must be significantly stronger statistical correlations between the measurement results at the three different points in time. If an object is actually in different states at the same time between the measurement times, this must—according to Leggett and Garg—lead to stronger correlations between the three measurements.
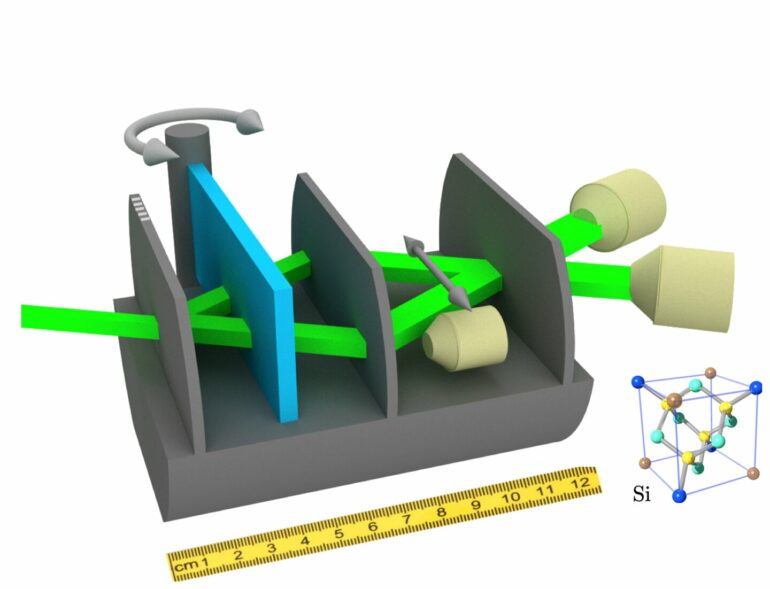
Neutron beams: Centimeter-sized quantum objects
“However, it is not so easy to investigate this question experimentally,” says Richard Wagner. “If we want to test macroscopic realism, then we need an object that is macroscopic in a certain sense, i.e. that has a size comparable to the size of our usual everyday objects.” At the same time, however, it must be an object that has a chance of still showing quantum properties.
“Neutron beams, as we use them in a neutron interferometer, are perfect for this,” says Hartmut Lemmel, instrument responsible at the S18 instrument at the Institut Laue-Langevin (ILL) in Grenoble, where the experiment was conducted.
In the neutron interferometer, a silicon perfect crystal interferometer that was first successfully used at the Atomic Institute of TU Wien in the early 1970s, the incident neutron beam is split into two partial beams at the first crystal plate and then recombined by another piece of silicon. There are therefore two different ways in which neutrons can travel from the source to the detector.
“Quantum theory says that every single neutron travels on both paths at the same time,” says Niels Geerits. “However, the two partial beams are several centimeters apart. In a sense, we are dealing with a quantum object that is huge by quantum standards.”
Using a sophisticated combination of several neutron measurements, the team at TU Wien was able to test the Leggett-Garg inequality—and the result was clear: the inequality is violated.
The neutrons behave in a way that cannot be explained by any conceivable macroscopically realistic theory. They actually travel on two paths at the same time, they are simultaneously located at different places, centimeters apart. The idea that “maybe the neutron is only traveling on one of the two paths, we just don’t know which one” has thus been refuted.
“Our experiment shows: Nature really is as strange as quantum theory claims,” says Stephan Sponar. “No matter which classical, macroscopically realistic theory you come up with: It will never be able to explain reality. It doesn’t work without quantum physics.”
More information:
Elisabeth Kreuzgruber et al, Violation of a Leggett-Garg Inequality Using Ideal Negative Measurements in Neutron Interferometry, Physical Review Letters (2024). DOI: 10.1103/PhysRevLett.132.260201. On arXiv: DOI: 10.48550/arxiv.2307.04409
Provided by
Vienna University of Technology
Citation:
Neutrons on classically inexplicable paths: Quantum theory prevails in Leggett-Garg inequality test (2024, July 2)