As scientists and researchers increasingly look to quantum computing to aid in complex problem-solving and advance our understanding of the universe—quantum error correction has become a critical area of scientific inquiry.
Increasing the accuracy and reliability of quantum computers is essential as scientists explore their practical applications—both for fundamental science and future technological applications.
New research published in Nature Physics on September 3, 2024 documents the discovery of a new way to separate nontrivial quantum error correction codes from trivial ones.
The research shows that this new boundary line isn’t arbitrary, and therefore represents fundamental progress on how quantum systems work in the real world. It paves the way for future applications not just in quantum computing—but also in condensed matter (with regards to topological order) and quantum gravity (with regards to conformal field theories).
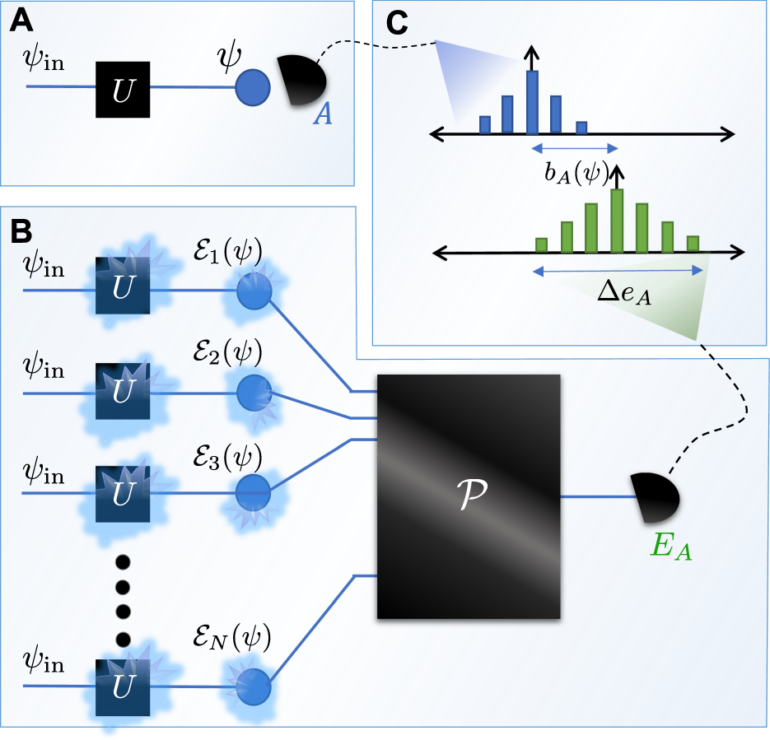
In their article, researchers Jinmin Yi, Weicheng Ye, Daniel Gottesman and Zi-Wen Liu—who have each been supported in their work by Perimeter—detail their discovery of a mathematically rigorous connection between Approximate Quantum Error Correction (AQEC) code properties and the complexity of quantum circuits. Using this connection, scientists can now evaluate the precision level of the quantum code.
Additionally, the researchers’ discovery that AQEC codes emerge naturally could help answer some of physics’ biggest, most challenging questions.
“This new dividing line that we’re proposing between acceptable and unacceptable codes corresponds to something physically meaningful,” said Dr. Daniel Gottesman, a longtime Perimeter faculty member and current Co-Director of the Joint Center for Quantum Information and Computer Science at the University of Maryland. “It shows that this was not just some random thing that we came up with, but that it’s connected to something fundamental.”
The discovery has applications in several fields of study. For example, researchers studying topological order—which explores the intricate properties of quantum materials like fractional quantum Hall states and certain superconductors—have long wrestled with the gap between entanglement conditions and code properties. These scientists now have the tools to better understand the relationship between these conditions, and advance our understanding of unique materials.
Jinmin Yi, a Perimeter PHD student and co-author of the paper, says that their research has provided “a quantitative understanding of why these two notions are actually different,” unlocking potential for future research.
The study of AQECs has also uncovered intriguing insights for scientists who are looking to integrate quantum mechanics with Einstein’s theory of general relativity—one of physics’ most persistent challenges. Specifically, evaluating AQECs using subsystem variance has indicated that certain Conformal Field Theory systems are more likely to integrate with gravitational descriptions.
While each of these areas deserves further study, the initial results are encouraging, and invite future exploration into the scope and utility of AQEC, along with its physical and practical applications.
More information:
Jinmin Yi et al, Complexity and order in approximate quantum error-correcting codes, Nature Physics (2024). DOI: 10.1038/s41567-024-02621-x
Provided by
Perimeter Institute for Theoretical Physics
Citation:
Quantum error correction research reveals fundamental insights into quantum systems (2024, September 4)