Topological synchronization of chaotic systems

Can we find order in chaos? Physicists have shown, for the first time that chaotic systems can synchronize due to stable structures that emerge from chaotic activity. These structures are known as fractals, shapes with patterns which repeat over and over again in different scales of the shape. As chaotic systems are being coupled, the fractal structures of the different systems will start to assimilate with each other, taking the same form, causing the systems to synchronize.

If the systems are strongly coupled, the fractal structures of the two systems will eventually become identical, causing complete synchronization between the systems. These findings help us understand how synchronization and self-organization can emerge from systems that didn’t have these properties to begin with, like chaotic systems and biological systems.

One of the biggest challenges today in physics is to understand chaotic systems. Chaos, in physics, has a very specific meaning. Chaotic systems behave like random systems. Although they follow deterministic laws, their dynamics still will change erratically. Because of the well-known “butterfly effect” their future behavior is unpredictable (like the weather system, for example).

Although chaotic systems seem random, they are not, and we can find order in chaos. From chaotic activity emerges a strange new structure or pattern known as a strange attractor. If enough time passes, every chaotic system will attract its unique strange attractor and will stay in this pattern. What’s strange about these patterns is that they are composed of fractals, structures with the same patterns repeating over and over again in different scales of the fractal (much like a branching structure of a tree, for example.). In fact, strange attractors are usually composed from multiple fractal structures. Different sets of states of the strange attractor will be part of different fractals and although the system will jump erratically from state to state, these fractals will stay stable throughout the chaotic activity of the system.

Because of the butterfly effect, chaotic systems seem to defy synchrony. Their extreme erratic behavior suggests that two coupled chaotic systems cannot be synchronized and have the same activity. Yet, physicists discovered in the 80’s that chaotic systems do synchronize. But how can that be?

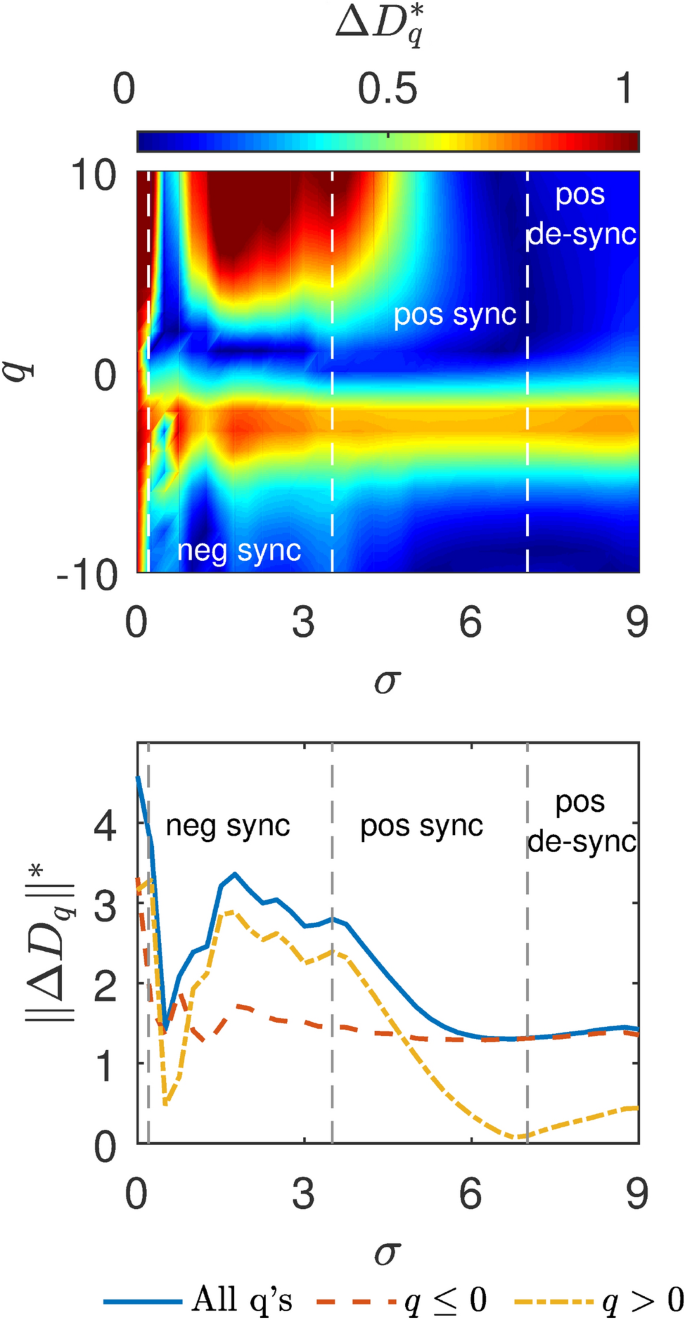
A study by a group of physicists from Bar–Ilan University in Israel, recently published in the journal Scientific Reports, suggests a new answer to this puzzling question. According to the research, led by Dr. Nir Lahav, the emergence of the stable fractals is the key element that gives chaotic systems the ability to synchronize. They showed that as chaotic systems are being coupled, the fractal structures start to assimilate each other causing the systems to synchronize. If the systems are strongly coupled, the fractal structures of the two systems will eventually become identical, causing a complete synchronization between the systems. They termed this phenomenon Topological Synchronization. In low coupling, only small amounts of the fractal structures will become the same, and as the coupling between the systems grows, more fractal structures will become identical.

To their surprise, the physicists found that there is a specific trait for the process of how fractals from one system take similar form of the fractals from the other. They discovered that in completely different chaotic systems this process maintains the same form. When the two chaotic systems are weakly coupled, the process usually starts with only particular fractal structures becoming identical. These are sets of sparse fractals that rarely will emerge from the activity of the chaotic system.

Synchronization starts when these rare fractals take a similar form in both systems. To get complete synchronization there must be a strong coupling between the systems. Only then will dominant fractals, that emerge most of the time from the system’s activity, also become the same. They called this process the Zipper Effect, because when describing it mathematically, it seems that as coupling between chaotic systems becomes stronger, it will gradually “zip up” more fractals to be the same.

These findings help us understand how synchronization and self-organization can emerge from systems that didn’t have these properties to begin with. For example, observing this process revealed new insights about chaotic synchronization in cases that were never studied before. Usually, physicists study synchronization between similar chaotic systems with small change of parameters between them. Using topological synchronization, the group managed to expand the study of synchronization to extreme cases of chaotic systems that have a big difference between their parameters. Topological synchronization might even help us shed light on how neurons in the brain synchronize with each other. There is some evidence that neural activity in the brain is chaotic. If so, topological synchronization can describe how synchronization emerges from the vast neural activity of the brain using the stable fractal structures.