A shard of smooth bone etched with irregular marks dating back 20,000 years puzzled archaeologists until they noticed something unique – the etchings, lines like tally marks, may have represented prime numbers. Similarly, a clay tablet from 1800 B.C.E. inscribed with Babylonian numbers describes a number system built on prime numbers.
As the Ishango bone, the Plimpton 322 tablet and other artifacts throughout history display, prime numbers have fascinated and captivated people throughout history. Today, prime numbers and their properties are studied in number theory, a branch of mathematics and active area of research today.
A history of prime numbers

Some scientists guess that the markings on the Ishango bone represent prime numbers.
Joeykentin/Wikimedia Commons, CC BY-SA
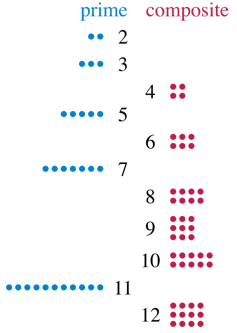
Informally, a positive counting number larger than one is prime if that number of dots can be arranged only into a rectangular array with one column or one row. For example, 11 is a prime number since 11 dots form only rectangular arrays of sizes 1 by 11 and 11 by 1. Conversely, 12 is not prime since you can use 12 dots to make an array of 3 by 4 dots, with multiple rows and multiple columns. Math textbooks define a prime number as a whole number greater than one whose only positive divisors are only 1 and itself.
Math historian Peter S. Rudman suggests that Greek mathematicians were likely the first to understand the concept of prime numbers, around 500 B.C.E.
Around 300 B.C.E., the Greek mathematician and logician Euclid proved that there are infinitely many prime numbers. Euclid began by assuming that there is a finite number of primes. Then he came up with a prime that was not on the original list to create a contradiction. Since a fundamental principle of mathematics is being logically consistent with no contradictions, Euclid then concluded that his original assumption must be false. So, there are infinitely many primes.
The argument established the existence of infinitely many primes, however it was not particularly constructive. Euler had no efficient method to list all the primes in an ascending list.
Prime numbers, when expressed as that number of dots, can be arranged only in a single row or column, rather than a square or rectangle.
David Eppstein/Wikimedia Commons
In the middle ages, Arab mathematicians advanced the Greeks’ theory of prime numbers, referred to as hasam numbers during this time. The Persian mathematician Kamal al-Din al-Farisi formulated the fundamental theorem of arithmetic, which states that any positive integer larger than one can be expressed uniquely as a product of primes.
From this view, prime numbers are the basic building blocks for constructing any positive whole number using multiplication – akin to atoms combining to make molecules in chemistry.
Prime numbers can be sorted into different types. In 1202, Leonardo Fibonacci introduced…


