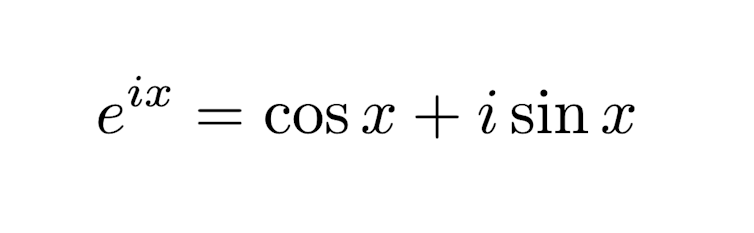To a nonmathematician, having the letter “i” represent a number that does not quite exist and is “imaginary” can be hard to wrap your head around. If you open your mind to this way of thinking, however, a whole new world becomes possible.
I’m a mathematician who studies analysis: an area of math that deals with complex numbers. Unlike the more familiar real numbers – positive and negative integers, fractions, square roots, cube roots and even numbers such as pi – complex numbers have an imaginary component. This means they are made of both real numbers and the imaginary number i: the square root of negative 1.
Remember, a square root of a number represents a number whose square is the original number. A positive number times itself is a positive number. A negative number times itself is a positive number. The imaginary number i depicts a number that somehow when multiplied by itself is negative.
Conversations about imaginary numbers with a nonmathematician often lead to objections like, “But those numbers don’t really exist, do they?” If you are one of these skeptics, you’re not alone. Even mathematical giants found complex numbers difficult to swallow. For one, calling -√1 “imaginary” isn’t doing it any favors in helping people understand that it’s not fantastical. Mathematician Girolamo Cardano, in his 1545 book dealing with complex numbers, “Ars Magna,” dismissed them as “subtle as they are useless.” Even Leonhard Euler, one of the greatest mathematicians, supposedly computed √(-2) √(-3) as √6. The correct answer is -√6.
In high school, you may have encountered the quadratic formula, which gives solutions to equations where the unknown variable is squared. Maybe your high school teacher didn’t want to deal with the issue of what happens when (b2 – 4ac) – the expression under the square root in the quadratic formula – is negative. They might have brushed this under the rug as something to deal with in college.
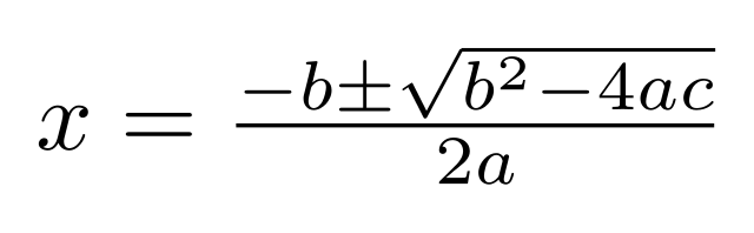
The quadratic formula can be applied in more cases when the expression under the radical is allowed to be negative.
Jamie Twells/Wikimedia Commons
However, if you are willing to believe in the existence of square roots of negative numbers, you will get solutions to a whole new set of quadratic equations. In fact, a whole amazing and useful world of mathematics comes into view: the world of complex analysis.
Complex numbers simplify other areas of math
What do you get for your leap of faith in complex numbers?
For one, trigonometry becomes a lot easier. Instead of memorizing several complicated trig formulas, you need only one equation to rule them all: Euler’s 1740 formula. With decent algebra skills, you can manipulate Euler’s formula to see that most of the standard trigonometric formulas used to measure a triangle’s length or angle become a snap.