Artificial neural networks are known to be highly efficient approximators of continuous functions, which are functions with no sudden changes in values (i.e., discontinuities, holes or jumps in graph representations). While many studies have explored the use of neural networks for approximating continuous functions, their ability to approximate nonlinear operators has rarely been investigated so far.
Researchers at Brown University recently developed DeepONet, a new neural network-based model that can learn both linear and nonlinear operators. This computational model, presented in a paper published in Nature Machine Intelligence, was inspired by a series of past studies carried out by a research group at Fudan University.
George Em Karniadakis, one of the researchers who carried out the study, told TechXplore, “About five years ago, as I was in class teaching variational calculus, I asked myself if a neural network can approximate a functional (we know it approximates a function). I searched around and found nothing, until one day I stumbled on a paper by Chen & Chen published in 1993, where the researchers achieved functional approximation using a single layer of neurons. Eventually, I also read another paper by the same team on operator regression, which we used as a starting point for our study. Since then, Prof T Chen has contacted me by email and thanked me for discovering his forgotten papers.”
Inspired by the papers by Chen and Chen at Fudan University, Karniadakis decided to explore the possibility of developing a neural network that could approximate both linear and nonlinear operators. He discussed this idea with one of his Ph.D. students, Lu Lu, who started developing DeepONet.
In contrast with conventional neural networks, which approximate functions, DeepONet approximates both linear and nonlinear operators. The model comprises two deep neural networks: one network that encodes the discrete input function space (i.e., branch net) and one that encodes the domain of the output functions (i.e., trunk net). Essentially, DeepONet takes functions as inputs, which are infinite dimensional objects, and maps them to other functions in the output space.
“With standard neural networks, we approximate functions, which take data points as input and outputs data points,” Karniadakis said. “So DeepOnet is a totally new way of looking at neural networks, as its networks can represent all known mathematical operators, but also differential equations in a continuous output space.”
Once it learns a given operator, DeepONet can complete operations and make predictions faster than other neural networks. In a series of initial evaluations, Karniadakis and his colleagues found that it could make predictions in fractions of a second, even those related to very complex systems.
“DeepONet can be extremely useful for autonomous vehicles, as it can make predictions in real time,” Karniadakis said. “It could also be used as a building block to simulate digital twins, systems of systems, and even complex social dynamical systems. In other words, the networks we developed can represent black-box complex systems after intense offline training.”
As part of their study, the researchers investigated different formulations of DeepONet’s input function space and assessed the impact of these formulations on the generalization error for 16 distinct applications. Their findings are highly promising, as their model could implicitly acquire a variety of linear and nonlinear operators.
In the future, DeepONet could have a wide range of possible applications. For instance, it could enable the development of robots that can solve calculus problems or solve differential equations, as well as more responsive and sophisticated autonomous vehicles.
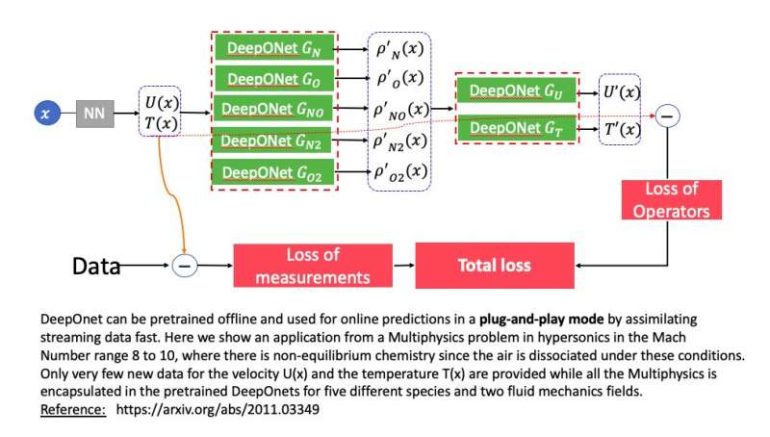
“I am now collaborating with labs from the Department of Energy and also with many industries to apply DeepONet to complex applications, e.g., in hypersonics, in climate modeling such as applications to model ice-melting in Antarctica, and in many design applications.”
Research shows the intrinsically nonlinear nature of receptive fields in vision
More information:
Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nature Machine Intelligence(2021). DOI: 10.1038/s42256-021-00302-5.
2021 Science X Network
Citation:
DeepONet: A deep neural network-based model to approximate linear and nonlinear operators (2021, April 12)
retrieved 12 April 2021
from https://techxplore.com/news/2021-04-deeponet-deep-neural-network-based-approximate.html
This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no
part may be reproduced without the written permission. The content is provided for information purposes only.