Spacetime is a conceptual model that fuses the three dimensions of space (length, width, and breadth) with the fourth dimension of time. By doing so, a four-dimensional geometric object is created. Researchers have recently used a similar way of thinking to study AI environments, leading to a unique reframing of AI problems in geometric terms.
Dr. Thomas Burns, a Ph.D. graduate and Visiting Researcher at the Okinawa Institute of Science and Technology (OIST), and Dr. Robert Tang, a mathematician at Xi’an Jiaotong-Liverpool University and a former post-doctoral researcher at OIST, wanted to study AI systems from a geometric perspective to more accurately represent their properties.
They have determined that the occurrence of a “geometric defect,” a failure of what is called Gromov’s Link Condition, correlates exactly to where there is potential for collision between moving AI agents. Their findings have been published in the journal Transactions on Machine Learning Research.
Modeling real-world scenarios with gridworlds
A gridworld is made up of square cells arranged in a grid, where cells can be occupied or not by a single agent, such as a koala, or an object, such as a beach ball. Agents in a gridworld can be programmed to solve puzzles and pursue rewards. They may move between adjacent tiles in the grid, and researchers often study their movements, planning, and strategies when they are tasked with specific goals, such as reaching a precise location in the gridworld.
Gridworlds have been long used in AI research, particularly in reinforcement learning, which has been used to beat world champions in video games and board games such as chess and Go. They provide simple yet scalable models for potential real-world applications, for example, safely coordinating the movements of autonomous cars or warehouse robots.
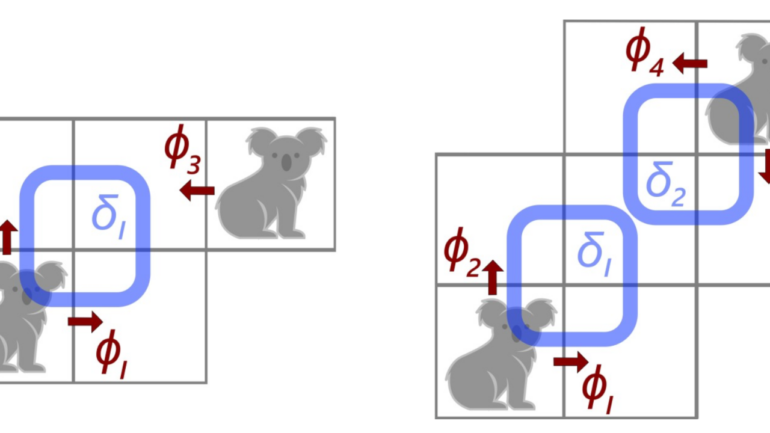
Starting at a chosen state in the gridworld—a specified arrangement of the agent(s) and object(s)—two actions were allowed: Move—letting an agent move to an adjacent empty cell, and Push/Pull—letting an agent push or pull an object in a straight line.
When this process is repeated enough times, a ‘state complex’ can be created. State complexes represent all possible configurations of a system as a single geometric object, which means we can study them using mathematical tools from geometry (concerning the precise shape of objects), topology (properties of spaces preserved under deformations, such as bending, stretching, and shrinking), and combinatorics (counting and arrangements of objects).
The researchers used a combination of pen-and-paper mathematics and a custom-made computer program to create and analyze the state complexes created in this study.
“It’s like a retro arcade game, but you can add all sorts of things, like doors, buttons, and enemies, and then think about the geometry and topology of any of these more complicated scenarios,” Dr. Burns explained. “You can intuitively think about the state complex as a physical Lego set with cubes, squares, and sticks stuck together, each representing specific reconfigurations of the gridworld.”
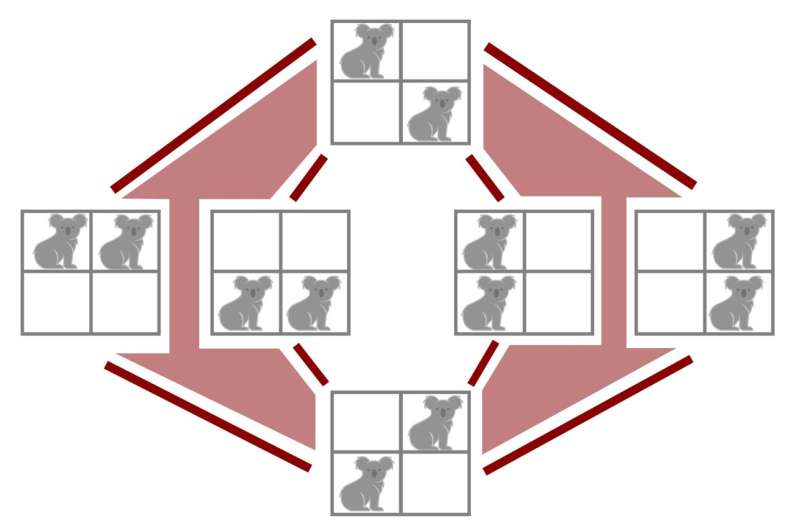
State complex of a 2 × 2 gridworld with two agents. Shading indicates squares attached to the surrounding 4–cycles. © Detecting danger in gridworlds using Gromov’s Link Condition, Transactions on Machine Learning Research (2024).
The moment before the collision
When two agents get too close together, they could potentially bump into each other. It turns out that this potential crash indicates a geometric defect, and every time it occurs in a gridworld, there could potentially be a collision.
Interestingly, most of the time, mathematicians aim to prove that an object like this does not have any geometric defects. This is because the absence of these defects is what gives the object desirable mathematical properties. If even a single geometric defect is present, then the whole state complex loses these benefits.
“Initially, we wanted to show that there were no geometric defects, but then we found heaps of these little annoyances, and we thought maybe it’s not so annoying, maybe it correlates with something important. It turns out yes, it is—it’s linked to this key safety information,” Dr. Burns said.
The scientists also proved that these geometric defects occur in the state complex when two agents are separated by a knight’s move or a two-step bishop’s move in chess. “These are the only cases when these defects occur. For instance, in the real world, robots could potentially bump into each other in a warehouse, or autonomous cars could collide at an intersection. It’s not the point of collision; it’s the moment before the collision that’s important.”
Practical applications for AI
Geometric defects and geometric methods in general can help improve our understanding of existing AI systems. For example, researchers could take an AI system trained to avoid collisions between agents and try to discover where these geometric defects lie. This may help scientists more efficiently detect potential collisions in AI systems, such as assisted living scenarios where robots and humans frequently interact.
“These findings provide a new method for seeking guaranteed safety limitations in AI environments with multiple agents—and they don’t need to be koalas; they could be robots helping with domestic tasks, exploring disaster zones, or autonomous vehicles for delivery services,” Dr. Burns noted.
More information:
Robert Tang et al, Detecting danger in gridworlds using Gromov’s Link Condition, Transactions on Machine Learning Research (2024). openreview.net/pdf?id=t4p612DftO
Provided by
Okinawa Institute of Science and Technology
Citation:
Enter the gridworld: Using geometry to detect danger in AI environments (2024, February 27)