A team of scientists has developed a novel hybrid scheme for both steady and unsteady single-phase compressible flow simulations. Their scheme has potential applications in real-world scenarios, offering a promising avenue for future research.
The team used a finite volume method called monotonic upstream-centered schemes for conservation laws (MUSCL) to create a novel scheme. Their novel scheme offers a more precise and high-resolution alternative to conventional MUSCL for compressible flow computations.
Their work was published in the journal Physics of Fluids on April 10, 2024.
Finite volume methods are numerical methods that scientists use to solve fluid dynamics problems. MUSCL is a finite volume method that can provide accurate numerical solutions for partial differential equations.
Scientists use compressible flow simulations to study compressible flow of gases that experience significant changes in their density. These numerical simulations can be used to solve many kinds of research problems, ranging from aerospace or mechanical engineering. Yet it has been challenging for scientists to accurately simulate flows because of complex phenomena, such as shock waves and discontinuities.
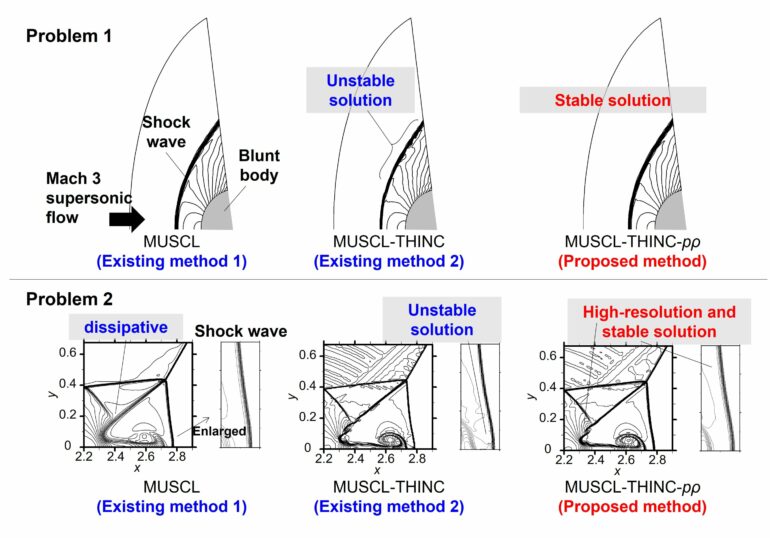
MUSCL is especially useful in aerospace engineering because of its straightforward mathematical expression and accuracy in fundamental flows featuring shock waves. However, it often produces dissipative solutions for complex flows, which deteriorate the accuracy of simulations.
“Although a lot of methods have been recently proposed, there is still a gap between the recently-developed, complex methods for academic interests and the widely-used methods that are actually used to handle engineering problems. To fill the gap and contribute to the engineering, we proposed a new method with accurate and stable simulations for compressible flows using simple expressions,” said Keiichi Kitamura, associate professor, Faculty of Engineering, Yokohama National University.
The research team used the MUSCL method along with the tangential hyperbolic interface capturing (THINC) method to create a novel hybrid scheme they call T-MUSCL. Their hybrid scheme optimizes the process based on the degree of nonlinearity and discontinuity around the target cells. They designed the scheme to provide an appropriate balance of nonlinearity between the physical phenomena and the reconstruction process. This solves the weak shock waves sharply and the strong shock waves robustly within the hybrid scheme.
The team used two key parameters: a nonlinearity-weighted parameter and a slope-ratio-weighted parameter. Their T-MUSCL scheme provides enhanced accuracy for continuous flow simulations with smaller errors than conventional MUSCL. It is capable of precisely capturing extremely weak moving and stationary shock waves. These cases were challenging for the conventional MUSCL to resolve accurately because of excessive numerical dissipation.
The T-MUSCL scheme also provides improved convergence behavior in steady two-dimensional blunt body problems and the lessening of unstable numerical behaviors in the presence of strong shock waves. This hybrid scheme can be easily adopted in place of conventional MUSCL in a range of practical applications without adding unnecessary complexity to existing algorithms.
“The punchline of the paper is that we obtained high-resolution and robust results for complex compressible flows using simple expressions. Our method is constructed within the so-called (spatially) second-order scheme, which is the most popular type of the numerical method. We believe that our method is accessible by a lot of users because of this feature,” said Kitamura.
Looking ahead, the researchers’ next step is to apply the proposed method to an actual engineering problem. They hope that their method will be widely used by researchers studying fluid dynamics. “Our ultimate goal is to deepen our understanding of compressible flow dynamics and shock waves by our method and contribute to accelerating the development in a variety of industries, such as aerospace and mechanical engineering,” said Gaku Fukushima, researcher, Faculty of Engineering, Yokohama National University.
More information:
Gaku Fukushima et al, Improved hybrid approach of monotonic upstream-centered scheme for conservation laws and discontinuity sharpening technique for steady and unsteady flows, Physics of Fluids (2024). DOI: 10.1063/5.0198163
Provided by
Yokohama National University
Citation:
Team develops novel hybrid scheme for compressible flow computations (2024, July 26)