Nonlinear systems have applications in many diverse fields from robotics to economics. Unlike linear systems, the output is not proportional to the input is such systems. A classic example is the motion of a pendulum. Due to the inherent nature of nonlinear systems, their mathematical modeling and, consequently, control is difficult.
In this context, the Takagi–Sugeno (T–S) fuzzy system emerges as a highly effective tool. This system leverages fuzzy logic to map input and output values to approximate a nonlinear system as multiple linear systems which are easier to model.
Fuzzy logic is a form of mathematical logic in which, instead of requiring all statements to be true (1) or false (0), the truth values can be any value between 0 and 1. T–S fuzzy system has thus served as the foundation for several nonlinear control methods, with the Parallel Distributed Compensator (PDC) method being the most prominent.
Furthermore, scientists have developed an enhanced version of this system, known as the fuzzy descriptor system (FDS). It combines the T–S fuzzy system with the powerful space–state representation, which describes a physical system in terms of state variables, input variables, and output variables.
Despite extensive research, optimal control strategies in the context of T–S FDSs are still largely unexplored. Additionally, while robust control methods, which protect against disturbances, have been explored for T–S FDS using methods like Linear Matrix Inequalities (LMI), these methods introduce additional complexity and optimization challenges.
To overcome these limitations, a group of researchers, led by Associate Professor Ngoc-Tam Bui from the Innovative Global Program of the College of Engineering at Shibaura Institute of Technology in Japan and including Thi-Van-Anh Nguyen, Quy-Thinh Dao, and Duc-Binh Pham, all from Hanoi University of Science and Technology, developed novel optimal and robust-optimal controllers based on the T–S fuzzy descriptor model. Their study was published in the journal Scientific Reports.
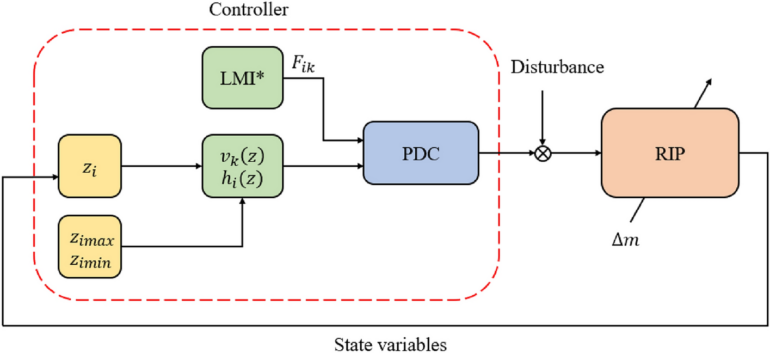
To develop the controllers, the team first utilized the powerful Lyapunov stability theory to establish the stability conditions for the mathematical model of the FDS. However, these stability conditions cannot be directly used. As Dr. Bui explains, “The stability conditions for the FDS model make it difficult to solve using established mathematical tools. To make them more amenable, we systematically transformed them into LMI.”
These modified conditions formed the basis for developing three controllers: the stability controller which uses PDC to manage deviations, the optimal controller which minimizes a cost function to obtain optimal control, and the robust-optimal controller which combines the benefits of both of them.
The researchers demonstrated the effectiveness of these controllers in controlling a rotary inverted pendulum, a challenging system comprising an inverted pendulum sitting on a rotating base. The problem is to keep the pendulum upright by controlling the rotation of the base.
The researchers tested the performance of the controllers using distinct simulation scenarios. Simulations revealed that the stability controller effectively stabilized the system when the initial displacement angle was small, while with larger initial angles, there were more oscillations, and the settling time was higher.
The high settling time was effectively addressed by the optimal controller, reducing it from 13 to 2 seconds, representing a six-fold reduction. Moreover, it also reduced the maximum amplitudes during oscillations.
The robust-optimal controller was tested using two different scenarios. In the first case, the mass of the pendulum bar was changed, while in the second, white noise was introduced into the control input. Compared to the optimal controller, it performed the same in the first scenario. However, the controller was considerably better in the second scenario, showing no oscillations while the optimal controller showed clear oscillations. Notably, the robust-optimal controller showed the lowest error values.
These results highlight the adaptability and potential of these controllers in practical scenarios. “The research findings hold promising implications for various real-life applications where stable control in dynamic and uncertain environments is paramount. Specifically, autonomous vehicles and industrial robots can achieve enhanced performance and adaptability using the proposed controllers,” remarks Dr. Bui.
“Overall, our research opens avenues for advancing control strategies in various domains, ultimately contributing to more capable autonomous systems, making transportation safer, health care more effective, and manufacturing more efficient.”
More information:
Duc-Binh Pham et al, Robust-optimal control of rotary inverted pendulum control through fuzzy descriptor-based techniques, Scientific Reports (2024). DOI: 10.1038/s41598-024-56202-2
Provided by
Shibaura Institute of Technology
Citation:
Novel robust-optimal controllers based on fuzzy descriptor system (2024, April 8)